算法 #8期：树系列 - 给出N，求唯一BST的总数
问题定义 🔗︎
给定 N，找出可以用 1 到 N 的值制作的唯一 BST 的总数
用例:
输入: n = 3
输出: 5
For n = 3, preorder traversal of
- 1 2 3
- 1 3 2
- 2 1 3
- 3 1 2
- 3 2 1
输入: 4
输出: 14
问题分析 🔗︎
起初，我不太明白这个问题的意思。什么是 BST？它的定义是：任何节点的值都小于右子树的任何节点，大于左子树的任何节点。我想一开始觉得就一种可能。实际上也可能有多种情况。
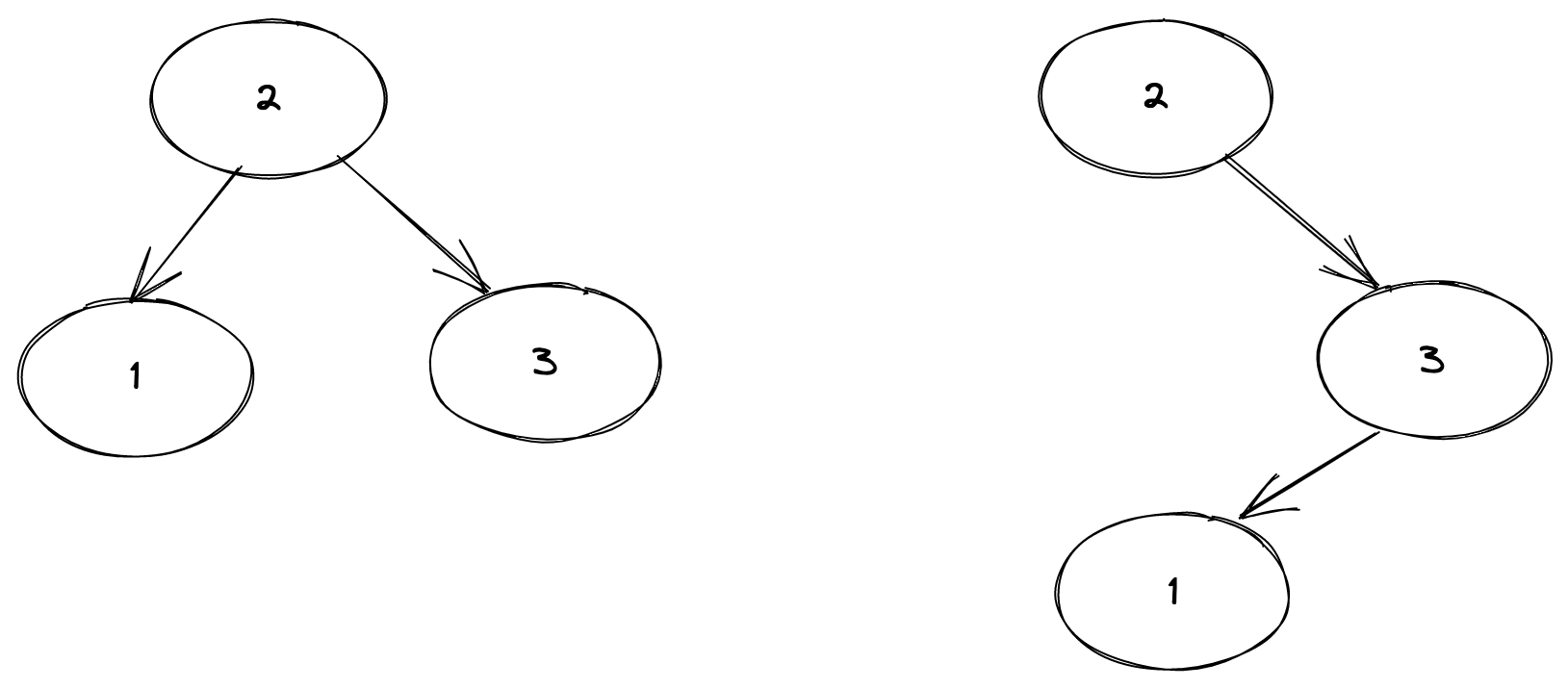
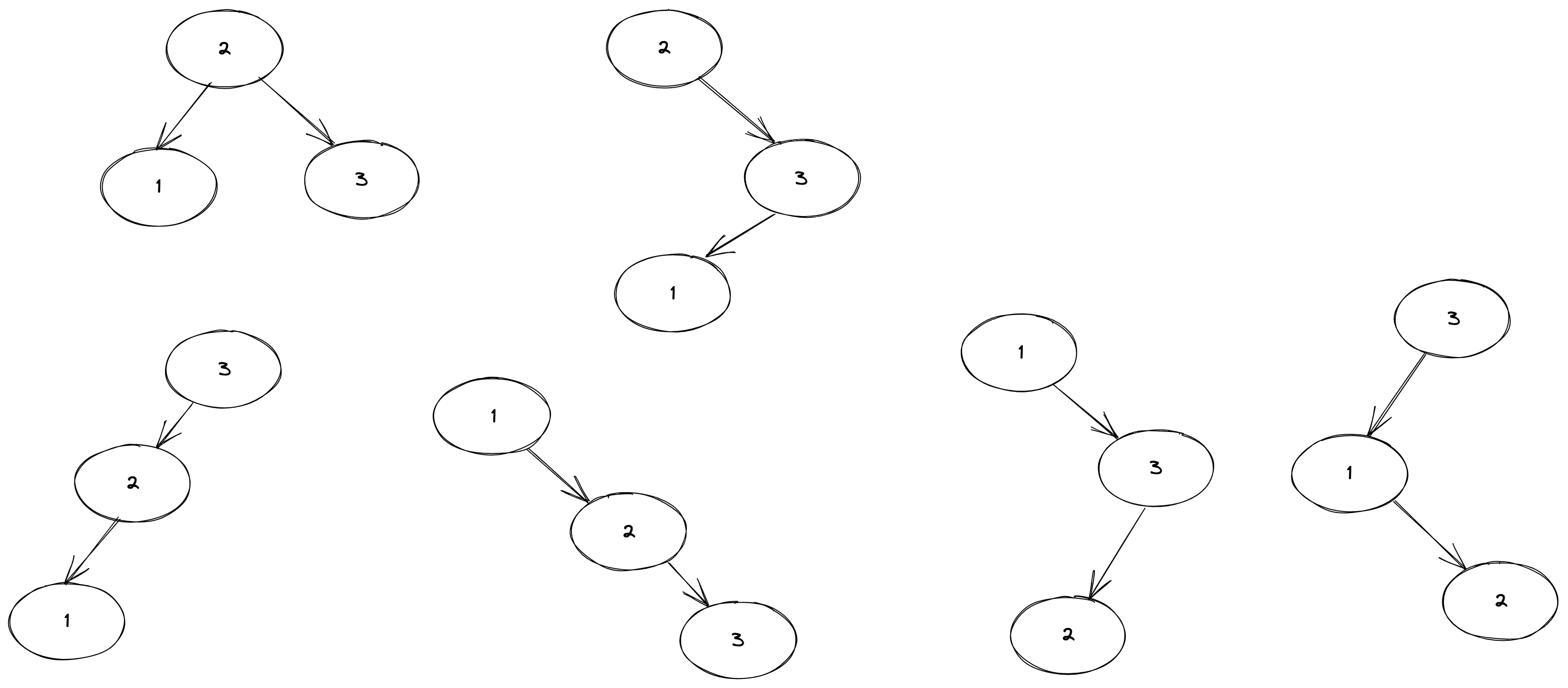
例如，给定节点 3 1 2，至少下面的排列可以满足 BST 的条件。
1 只有一个节点，显然只有一种情况。T(1) = 1
2 如果有两个节点，就有两种情况。T(2) = 2
3 如果有三个节点。
- 假设 1 是根节点，2 3 在根节点的右边，结果将是。 T(0) * T(2) ( 我们已经知道 T(2) = 2)
- 假设 2 是根节点，1 3 分别在两侧，结果将是。T(1) * T(1)
- 假设 3 是根节点，1 2 在根节点的左边，结果将是。T(2) * T(0) 这样，我们遍历了所有可能的情况。 T（2）+ T（1）+ T（2）= 2 + 1 + 2 = 5 所以结果是 5，这与问题定义中的案例结果一致
3 如果有 4 个节点，如 1 2 3 4，怎么办。还是按照上面的思路，有。
- T(0) * T(3), i = 1
- T(1) * T(2), i = 2
- T(2) * T(1), i = 3
- T(3) * T(0), i = 4
然后，把它们全部加起来： 5+2+2+5=14 对，结果是正确的
根据上面的分析，我们可以大概知道这个规律：假设 i 是根节点，T[i-1]*T[n-i]是当前情况下的 BST 树的数量。而最终 BST 树的数量是通过遍历所有作为根节点的节点，然后得到的。将它们的数量加在一起。
编码 🔗︎
暴力方案。采用递归
// i is the root, n is the total nodes' number
const G = (i, n) => {
return fn(i - 1) * fn(n - i);
};
// Get the total number of BST trees with n nodes.
const fn = (n) => {
let _ = 0;
if (n === 0 || n === 1) return 1;
for (let i = 1; i <= n; i++) {
_ += G(i, n);
}
return _;
};
console.log(fn(3));
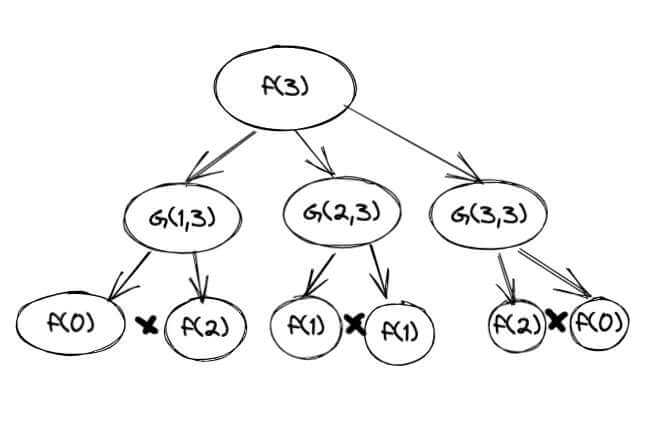
如果你以前学过 CS 课程，因为代码中都是递归的内容。我们可以画出递归树：f(3)是最终结果，3 个节点的数字。 G(1,3)表示 1 为根，3 为节点的总数。 我们还可以做一个结论。G(i, n) = f(i-1)*f(n-i)
从递归树中，我们还可以看到 f(1)f(2)f(0)是重复计算的，我们可以缓存这些数据以避免重复计算。
// get the total number of BST tress with i as the root node
const G = (i, n) => {
return fn(i - 1) * fn(n - i);
};
const dp = [];
const fn = (n) => {
let _ = 0;
if (n === 0 || n === 1) return 1;
if (dp[n]) {
console.log("hit cache");
return dp[n];
}
// loop all nodes
for (let i = 1; i <= n; i++) {
// add them all
_ += G(i, n);
}
// cache result
dp[n] = _;
return _;
};
console.log(fn(3));
应该有三个命中重复的，但我们只有一个。所以这样一来，我们就不能完全利用重复计算。我们可以从上到下进行决策。例如，在 i 为根的情况下，我们先以 i-1…1 为根的值进行计算。
优化结果如下:
const getNumberOfBSTs = (n) => {
const T = [];
T[0] = 1;
T[1] = 1;
for (let i = 2; i <= n; i++) {
// j form 1 to i represents the already calculated results
for (let j = 1; j <= i; j++) {
// This is the conclusion derived from the recursive tree above
T[i] += T[j - 1] * T[i - j];
}
}
};
时间复杂度 🔗︎
双层循环： O(n^2)