算法 #1期:搜索引擎的拼写纠错功能-莱文斯坦距离
案例 🔗︎
给定两个字符串,如何量化他们的相似度。 这里引出了“编辑距离”这个概念,就是将一个字符串转为另一个字符串,需要的最小的编辑操作次数。编辑次数 越少,则相似度越高。 比如我们有两个字符串: mitcmu 和 mtacnu. 他们的编辑距离是多少?
分析 🔗︎
一种方式还是列出所有的可能,通过回溯算法实现:
如果a[i]和a[j]匹配,则递归考察a[i+1]和b[j+1]
如果a[i]和b[j]不匹配,则有多个处理方式
1、删除a[i],递归考察a[i]和b[j+1],或者 删除b[j],递归考察a[i+1]和b[j]
2、添加:在a[i]前面添加一个与b[j]相同的字符,然后递归考虑a[i]和b[j+1];或者在b[j]前面添加一个与a[i]相等的字符,然后递归考察a[i+1]和b[j]
3、替换:将a[i]替换成b[j],或者将b[j]替换成a[i],然后递归考察a[i+1]和b[j+1]
这种方式是采用回溯算法,时间复杂度较高。我们对f(i,j,edit_dist)画出递归树,发现出现重复子节点,说明可以优化。 怎么优化,对于(i,j)相同的节点,我们只需要保留edit_dist更小的节点继续递归,其他节点可以舍弃。因此状态就从(i,j,edit_dist)变成了(i,j,min_edit_dist)。 min_edit_dist也就是我们的最小编辑操作次数,也就是a[0,i-1]转换为b[0,j-1]字符串的最小编辑次数。另外,通过递归树,我们发现,状态(i,j)可以从(i-1,j)、 (i, j - 1), (i-1, j-1)任意一个状态中转移过来。
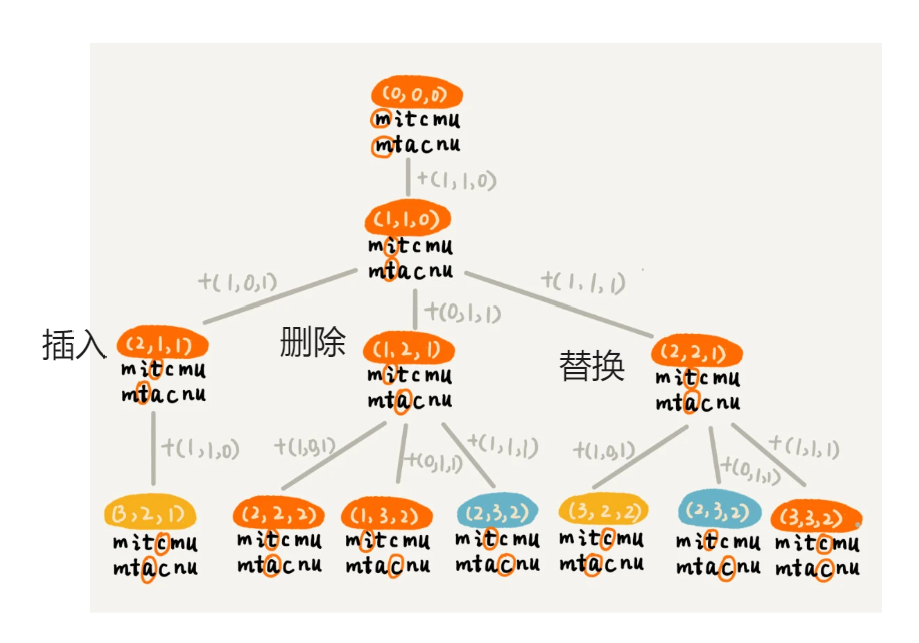
递归树
- 如果S的第i个字符等于T的第j个字符,则不需要进行任何操作,因此minDist[i][j] = minDist[i-1][j-1]。
- 如果S的第i个字符不等于T的第j个字符,则可以进行以下三种操作之一:
- 插入(Insertion):在S的第i个字符后插入T的第j个字符,这样S的前i个字符与T的前j+1个字符相等,因此minDist[i][j] = minDist[i][j-1] + 1。
- 删除(Deletion):删除S的第i个字符,这样S的前i-1个字符与T的前j个字符相等,因此minDist[i][j] = minDist[i-1][j] + 1。
- 替换(Substitution):将S的第i个字符替换为T的第j个字符,这样S的前i个字符与T的前j个字符相等,因此minDist[i][j] = minDist[i-1][j-1] + 1。
写出状态转移方程就是:
如果a[i-1] != b[j-1], 则minDist[i,j] = Min(minDist(i-1,j)+1, minDist(i,j-1)+1, minDist(i-1,j-1)+1)
如果a[i-1] == b[j-1], 则minDist[i,j] = minDist(i-1,j-1)
翻译成代码就是:
function lwstDP(a, n, b, m) {
const minDist = new Array(n + 1);
for (let i = 0; i < n + 1; i++) {
minDist[i] = new Array(m + 1);
minDist[i][0] = i;
}
for (let j = 0; j < m + 1; j++) {
minDist[0][j] = j;
}
for (let i = 1; i < n + 1; i++) {
for (let j = 1; j < m + 1; j++) {
if (a[i - 1] === b[j - 1]) {
minDist[i][j] = minOfThree(
minDist[i - 1][j] + 1,
minDist[i][j - 1] + 1,
minDist[i - 1][j - 1]
);
} else {
minDist[i][j] = minOfThree(
minDist[i - 1][j] + 1,
minDist[i][j - 1] + 1,
minDist[i - 1][j - 1] + 1
);
}
}
}
return minDist[n][m];
}
function minOfThree(n1, n2, n3) {
return Math.min(n1, Math.min(n2, n3));
}