算法 #2期:双11凑单问题 - 动态规划的使用
案例 🔗︎
假定我们的购物车有n件商品(价格已知),从这n件商品中挑出来,刚好满足满减要求的价格,比如200元。怎么挑选? 这个简化下: 比如我们商品是[2,2,4,6,3], 数组里存储的是商品价格,然后我们的满减要求是10元。
分析 🔗︎
这个问题最常规的做法,是可以通过列出所有的排列组合,然后找到满足要求的商品。这个思想本质上就是回溯思想。 但是这种解法如果商品数量很多,计算结果会很慢,因为时间复杂度是指数级的。 那有什么法子呢?
我们从背包问题得到启发,背包问题是在已知背包最大载重的情况下,从已知的物品里装最多的东西。 比如:我们已有商品items: [2,2,4,6,3] 不超过背包最大重量9的前提下,最多能放多重的物品。
同样的我们可以遍历每个排列组合,画出递归树,也就是每次决策节点是f(i,cw)。其中i表示决策第几个物品是否放入背包,cw(current weight)表示当前物品的重量。 通过这棵树,可以发现有一些重复节点(感兴趣的可以画下递归树,看下有多少个节点。对比下通过状态表它的复杂度)
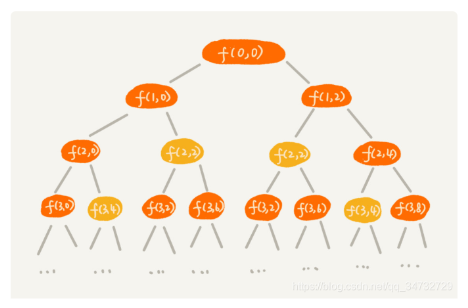
递归树
1、方法1: 通过每次记录重复节点(用备忘录,一个二维数组[商品个数][最大重量]),如果有值,则直接返回,而不是重复计算。
2、方法2: 通过状态表(一个二维数组[商品个数][最大重量])只记录不同的状态,基于上一层的状态集合来推导下一层的状态集合,这样能保证每一层 的状态个数不会超过w个(w是背包可承载的最大重量)

状态表填写过程
通过这两种方法,都可以避免状态的指数级增长。这里我们采用方法2(一般动态规划都这么干,更加普适)。 双11凑单问题也类似,本质上就是要选出的商品价格达到10。 这里假设我们上限是10*3,也就是商品价格总和超过30,超出太多我们就放弃买了
代码:
/**
* 双11凑单问题
* @param items 商品价格
* @param n 商品个数
* @param w 凑单金额
*/
function double11advance(items, n, w) {
// 以下代码和背包问题没差别
let states = new Array(n); // 初始化状态表
for (let i = 0; i < n; i++) {
states[i] = new Array(3 * w + 1).fill(false);
}
states[0][0] = true; // 首先第一次决策
if (items[0] <= 3 * w) {
states[0][items[0]] = true;
}
for (let i = 1; i < n; i++) {
for (let j = 0; j <= 3 * w; j++) { // 不选择
if (states[i - 1][j] === true) {
states[i][j] = states[i - 1][j]; // 状态保持不变和上一次一样
}
}
for (let j = 0; j <= 3 * w - items[i]; j++) { // 选择
if (states[i - 1][j] === true) {
states[i][j + items[i]] = true; // 标记该点位为已决策
}
}
}
// 以下部分和背包问题有差异
let j;
for (j = w; j < 3 * w + 1; j++) { // 找到最接近200的决策价格
if (states[n - 1][j] === true) {
break;
}
}
if (j === 3 * w + 1) { // 找不到这样的组合
return;
}
for (let i = n - 1; i >= 1; i--) { // 从第一个商品开始
// 从n个商品中检测,如果上一个标记点位[i-1, j-items[i]]标记是1表示是选择了该商品
if (j - items[i] > 0 && states[i - 1][j - items[i]] === true) {
console.log(items[i] + " ");// 打印已选商品
j = j - items[i];
}
}
if (j !== 0) { // 如果还有钱剩余,表示第0个商品也选了(因为我们状态表是从上一个状态推导到下一个)如果没有买第0个,到这里j == 0了,如果j不为0,说明买了第0个
console.log(items[0]);
}
}