算法 #7期:图系列 - 检测无定向图中的环
问题定义 🔗︎
给定一个无向图,如何检查图中是否有一个环 ?
用例 1:
输入:n = 4 , e = 4, the edges = { 0 1, 1 2, 2 3, 0 2 }
输出: yes
示例:
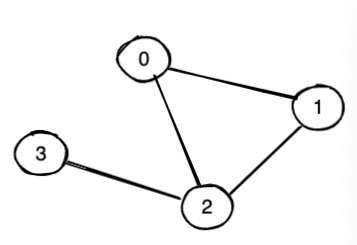
has circle
用例 2:
输入: n = 4, e = 3, the edges: { 0 1, 1 2, 2 3 }
输出: No
示例:
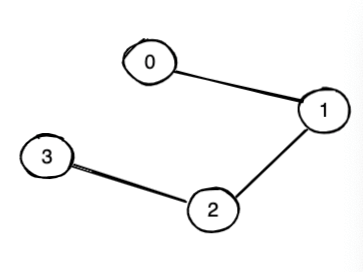
no circle
问题分析 🔗︎
我们都知道:
算法 + 数据结构 = 程序
因此,我们需要创建一个数据结构来代表无向图。有两种数据结构可以做到这一点:
- 邻接表 - 如果顶点 1 与顶点 2,3 相连,因此邻接表 : { 1 : [2, 4] }.
- 邻接矩阵 - JS 中我们可以用 map .
算法:如何检测环:
- 方案 1: 并查集 创建集合、合并、找到集合
- 最初,所有顶点都是不同的集合
- 然后我们循环所有边的节点,如果这些节点在不同的集合中,我们就联合它们。我们如何检查它们是否在同一个集合中,每个节点的父节点是现在的节点,那么它们就在同一个集合中。而代表节点的父节点是负数 n,n 代表它在其集合中有 n 个孩子。
- 如果这些节点都在同一个集合中,那么我们就知道它们有另一种方式可以到达对方,这意味着循环存在。
- 方案 2: 深度和广度遍历
- 我们需要一个被访问的队列,如果我们访问了一个节点,则设置为 visited。如果我们发现一个节点是当前节点的邻接节点,同时,它被访问过,那么我们发现了一个环
编码 🔗︎
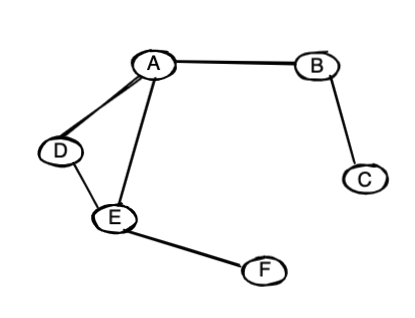
a graph
/*
Graph using adjacency list. Support opertaions:
1 traverse by dfs\bfs
2 hasCircleByDfs
3 hasCircleByBfs
4 hasCircleByDss(Disjoint Set)
*/
class Graph {
constructor() {
this.allVertexes = [];
this.allEdges = [];
this.adList = new Map();
}
addV(v) {
if (!this.adList.has(v)) {
this.adList.set(v, []);
}
this.allVertexes.push(v);
}
addE(source, dest) {
if (!this.adList.has(source)) {
this.addV(source);
}
if (!this.adList.has(dest)) {
this.addV(dest);
}
this.adList.get(source).push(dest);
this.adList.get(dest).push(source);
this.allEdges.push({
dest,
source,
});
}
removeV(v) {
for (let adV of this.adList.get(v)) {
this.removeE(v, adV);
}
this.adList.delete(v);
}
removeE(source, dest) {
this.adList.set(
source,
this.adList.get(source).filter((v) => v !== dest)
);
this.adList.set(
dest,
this.adList.get(dest).filter((v) => v !== source)
);
}
print() {
for (let v of this.adList.keys()) {
let cons = "";
for (let dest of this.adList.get(v)) {
cons += dest + " ";
}
console.log(v + " -> " + cons);
}
}
hasCircleByDss() {
const dss = new DisjointSet();
this.allVertexes.forEach((v) => {
dss.makeSet(v);
});
// if union return true, we find a cycle
return this.allEdges.some((e) => dss.union(e.source, e.dest));
}
bfs(start) {
const queue = [start];
const result = [];
const visited = {};
visited[start] = true;
let curV;
while (queue.length) {
curV = queue.shift();
result.push(curV);
this.adList.get(curV).forEach((dest) => {
if (!visited[dest]) {
visited[dest] = true;
queue.push(dest);
}
});
}
return result;
}
/*
Key Point: if we find a node is visited, but the node is not the current node's parent
*/
hasCircleByBfs() {
const parent = {};
const result = false;
const visited = {};
const queue = [];
for (let i = 0; i < this.allVertexes.length; i++) {
const node = this.allVertexes[i];
if (!visited[node]) {
visited[node] = true;
queue.push(node);
let curV;
while (queue.length) {
curV = queue.shift();
visited[curV] = true;
const allAdNodes = this.adList.get(curV);
for (let j = 0; j < allAdNodes.length; j++) {
const dest = allAdNodes[j];
if (!visited[dest]) {
visited[dest] = true;
parent[dest] = curV;
queue.push(dest);
} else if (dest !== parent[curV]) {
return true;
}
}
}
}
}
return false;
}
dfsRecursive(start) {
const result = [];
const visited = {};
const adList = this.adList;
(function dfs(v) {
if (!v) return null;
visited[v] = true;
result.push(v);
adList.get(v).forEach((dest) => {
if (!visited[dest]) {
return dfs(dest);
}
});
})(start);
return result;
}
dfsIterative(start) {
const result = [];
const visited = {};
const stack = [start];
let curV;
visited[start] = true;
while (stack.length) {
curV = stack.pop();
result.push(curV);
this.adList.get(curV).forEach((dest) => {
if (!visited[dest]) {
visited[dest] = true;
stack.push(dest);
}
});
}
return result;
}
/*
the key point is: all visited nodes are keep in array, if we repeated push a exsited node, there are more than one path to it(circle exists).
@params {string} current node
@params {array} boolean - all visited nodes
@params {string} parent - current node's parent
*/
hasCircleUtil(node, visited, parent) {
// push all nodes to visited
visited[node] = true;
const adList = this.adList.get(node) || [];
for (let i = 0; i < adList.length; i++) {
// the repeated path, ignore it
if (adList[i] === parent) continue;
// we find it is already in the visited queue, we know that. we can reach adList[i] by another path(which means there is a circle)
if (visited[adList[i]]) return true;
const hasCycle = this.hasCircleUtil(adList[i], visited, node);
if (hasCycle) return true;
}
return false;
}
hasCircleByDfs() {
const visited = {},
allV = this.allVertexes;
// because it is undirected graph, we need to reverse all nodes.
for (let i = 0; i < allV.length; i++) {
if (visited[allV[i]]) continue;
const flag = this.hasCircleUtil(allV[i], visited, null);
if (flag) return true;
}
return false;
}
}
/*
three operation:
1 makeset
2 find
3 union
*/
class DisjointSet {
constructor() {
this.map = new Map();
}
makeSet(data) {
this.map.set(data, -1);
}
find(x) {
const parent = this.map.get(x);
if (parent < 0) {
return x;
} else {
// recurse until you find x's parent
return this.find(this.map.get(x));
}
}
union(x, y) {
const xparent = this.find(x);
const yparent = this.find(y);
if (xparent !== yparent) {
// make the represent node's negative plus 1
this.map.set(xparent, this.map.get(xparent) + this.map.get(yparent));
// make y point to represents node x
this.map.set(yparent, xparent);
} else {
// same set
return true;
}
}
console_print() {
console.log(JSON.stringify(this.map.values()));
}
}
// test code
const g = new Graph();
var vertices = ["A", "B", "C", "D", "E", "F"];
// adding vertices
for (var i = 0; i < vertices.length; i++) {
g.addV(vertices[i]);
}
g.addE("A", "B");
g.addE("A", "D");
g.addE("B", "C");
g.addE("D", "E");
g.addE("E", "F");
g.addE("A", "E"); //circle path
g.print();
g.hasCircleByDss("A"); //true
g.hasCircleByDfs();
g.hasCircleByBfs();
时间复杂度 🔗︎
BFS/DFS: O(V+E)
DisjointSet: O(n) -> O(logn) using Rank