Algorithm #3: Partitioning algorithms in massive data
Case 🔗︎
We have 1TB of order data that needs to be sorted by dollar size. How can we solve this problem?
Analysis 🔗︎
This is a massive data processing problem, and the idea for this class can be through partitioning ideas, as our title says. What is partitioning? In simple terms, it means breaking down a problem into smaller, similar problems, solving each of these problems separately, and then combining the results of the smaller problems to get the final result. This is a bit abstract, but we can understand partitioning by looking at the case of subsumption sorting, which is relatively simple.
In simple terms, it means that a set of numbers is broken down continuously until the last set is considered to be sorted by only one number, and then each set is combined to obtain the final result:
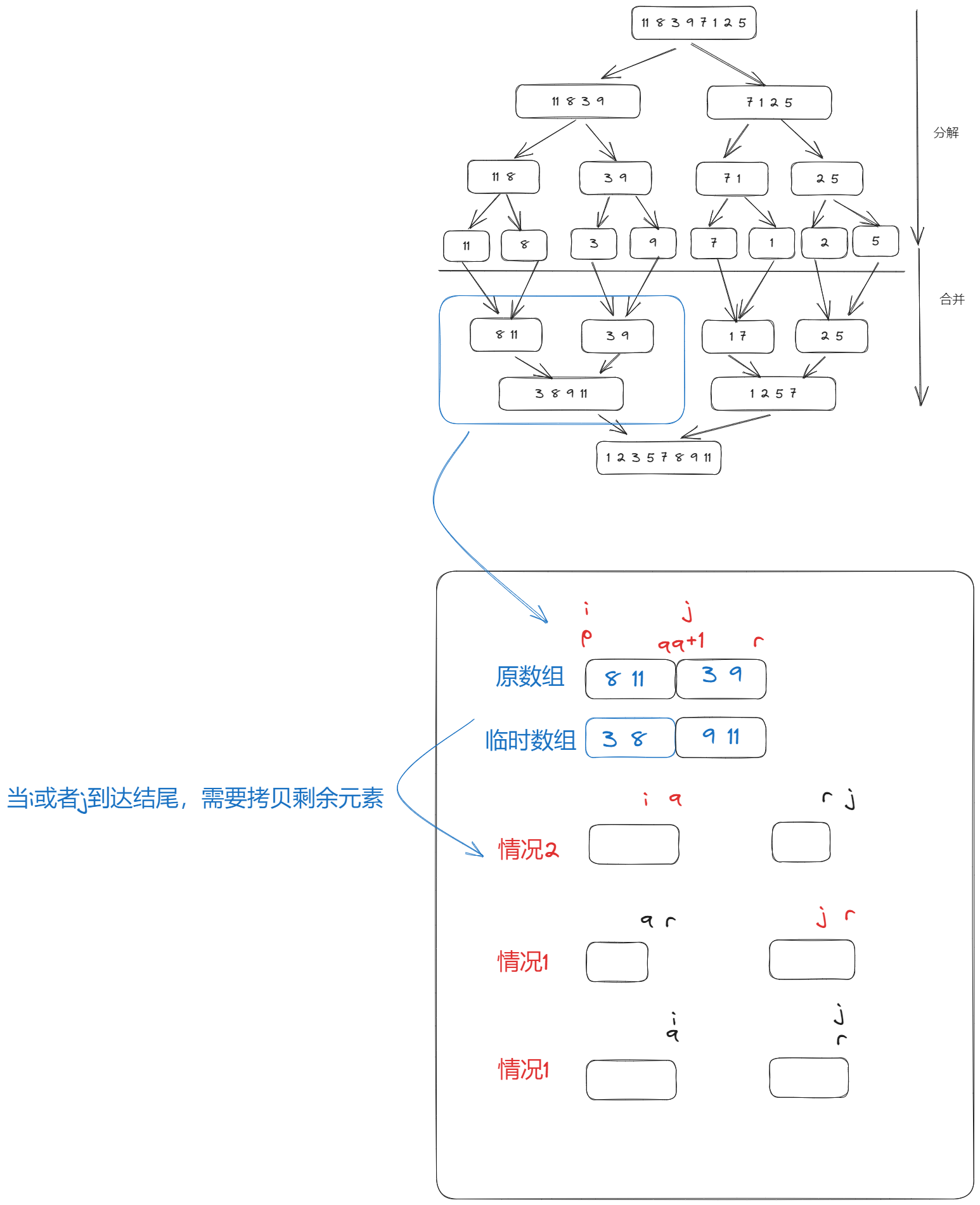
merge sort
This process of decomposition and merging is the idea of partitioning. The most important thing is how to merge, and the result must be sorted in ascending order. The process of merging is also very simple: assume that arrays A and B are merged and a new array is requested before each merge (the size of the array is A+B). Then use two cursors to point to A and B respectively, and copy the smaller one into the new array and move its cursor. If the cursor reaches the end of the array, the comparison stops and the remaining elements are copied to the new array (there will be two cases here, refer to the illustration) and finally the new array is copied to the original data (which will change the contents of the original array).
So the whole process of subsorting has only two arrays, one for the original array and one for the process of merging. The cursors all point to the original array.
const mergeSort = (data, p, r) => {
// 如果只剩一个元素,结束循环
if(p >= r) return;
// 暂且以中间为分割
let q = Math.floor((p + r) / 2);
// 分解
mergeSort(data, p, q)
mergeSort(data, q + 1, r)
// 合并
merge(data, p, q, r)
}
const merge = (data, p, q, r) => {
const temp = new Array(r-p+1);
let i = p;
let j = q+1;
let k = 0;
while(i<=q && j <= r) {
if(data[i] <= data[j]) {
temp[k++] = data[i++]
}
else {
temp[k++] =data[j++]
}
}
// 判断哪个数组中有剩余数据
let start = i;
let end = r;
if(j>r) {
end = q
}
else {
start = j
}
while(start <= end) {
temp[k++] = data[start++]
}
// 将temp复制回去
for(let i=0;i<r-p+1; i++) {
data[p+i] = temp[i]
}
return data;
}
export const ms_test_function = () => {
const data = [11,8,3,9,7,1,2,3]
mergeSort(data, 0, data.length - 1)
return true;
}
Back to the main topic. How to sort when faced with a large amount of order data and how to sort when the machine is short of memory.
- First of all, you have to read this large file line by line to a small file. How can the small file be split up. Mainly according to the amount of the order. For example, the maximum amount of the order is 10,000, we will split the amount 0-99, 100-199, 200-299 … 0 to 99 will be placed in file 0, 100-199 will be placed in file 1, and so on. Why split the files according to the amount. The main reason is to facilitate the merging of small files later on, so that they can be sorted according to the size of the file name.
// Step 1: Divide the file into smaller partitions based on order amounts
function partitionFile(inputFilePath, outputDirPath, callback) {
const partitions = {};
// Read the input file sequentially
const readStream = fs.createReadStream(inputFilePath, { encoding: 'utf8' });
readStream.on('data', (chunk) => {
const orders = chunk.split('\n');
orders.forEach((order) => {
// Extract the order amount from the order entry
const amount = parseFloat(order.split(',')[1]);
// Determine the partition for the order based on its amount
const partition = Math.floor(amount / 100);
// Create a writable stream for the partition file if it doesn't exist
if (!partitions.hasOwnProperty(partition)) {
const partitionFilePath = `${outputDirPath}/partition_${partition}.txt`;
partitions[partition] = fs.createWriteStream(partitionFilePath, { flags: 'a' });
}
// Write the order to the appropriate partition file
partitions[partition].write(`${order}\n`);
});
});
readStream.on('end', () => {
// Close all partition files
for (const partition in partitions) {
partitions[partition].end();
}
callback();
});
}
- each small file in memory sorting (here can be processed by a computer, but also by multiple computers in parallel, like google’s MapReduce ideas, can speed up the processing, of course, here also involves the scheduling of the machine problem), and write back to the small file
// Step 2: Sort each partition individually
function sortPartitions(inputDirPath, outputDirPath, callback) {
fs.readdir(inputDirPath, (err, files) => {
if (err) {
throw err;
}
files.forEach((file) => {
const filePath = `${inputDirPath}/${file}`;
const sortedFilePath = `${outputDirPath}/sorted_${file}`;
// Read the orders from the partition file
const orders = fs.readFileSync(filePath, { encoding: 'utf8' }).split('\n');
// Sort the orders using an efficient algorithm (e.g., merge sort)
const sortedOrders = orders.sort((a, b) => {
const amountA = parseFloat(a.split(',')[1]);
const amountB = parseFloat(b.split(',')[1]);
return amountA - amountB;
});
// Write the sorted orders to the sorted partition file
fs.writeFileSync(sortedFilePath, sortedOrders.join('\n'), { encoding: 'utf8' });
});
callback();
});
}
- Merge the small files into the large files according to the file name in accordance with the merge sort. This completes the sorting of the entire file.
// Step 3: Merge the sorted partitions
function mergePartitions(inputDirPath, outputFilePath) {
// Step 1: Perform merge sort on an array of numbers
function mergeSort(arr) {
if (arr.length <= 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
// Step 2: Merge two sorted arrays
function merge(left, right) {
let merged = [];
let i = 0;
let j = 0;
while (i < left.length && j < right.length) {
// 读取文件标题后面的数字
if (parseFloat(left[i].split(',')[1]) <= parseFloat(right[j].split(',')[1])) {
merged.push(left[i]);
i++;
} else {
merged.push(right[j]);
j++;
}
}
while (i < left.length) {
merged.push(left[i]);
i++;
}
while (j < right.length) {
merged.push(right[j]);
j++;
}
return merged;
}
const filePointers = [];
let mergedOutput = '';
fs.readdir(inputDirPath, (err, files) => {
if (err) {
throw err;
}
// Open all sorted partition files and initialize file pointers
files.forEach((file) => {
const filePath = path.join(inputDirPath, file);
const fileData = fs.readFileSync(filePath, 'utf8').trim();
const partitionData = fileData.split('\n');
filePointers.push(partitionData);
});
// Merge the sorted partitions
const sortedOutput = mergeSort(filePointers.flat());
// Format the sorted output
mergedOutput = sortedOutput.join('\n') + '\n';
// Write the merged output to the final sorted file
fs.writeFileSync(outputFilePath, mergedOutput, { encoding: 'utf8' });
// Delete the temporary partition files
// files.forEach((file) => {
// const filePath = path.join(inputDirPath, file);
// fs.unlinkSync(filePath);
// });
});
}
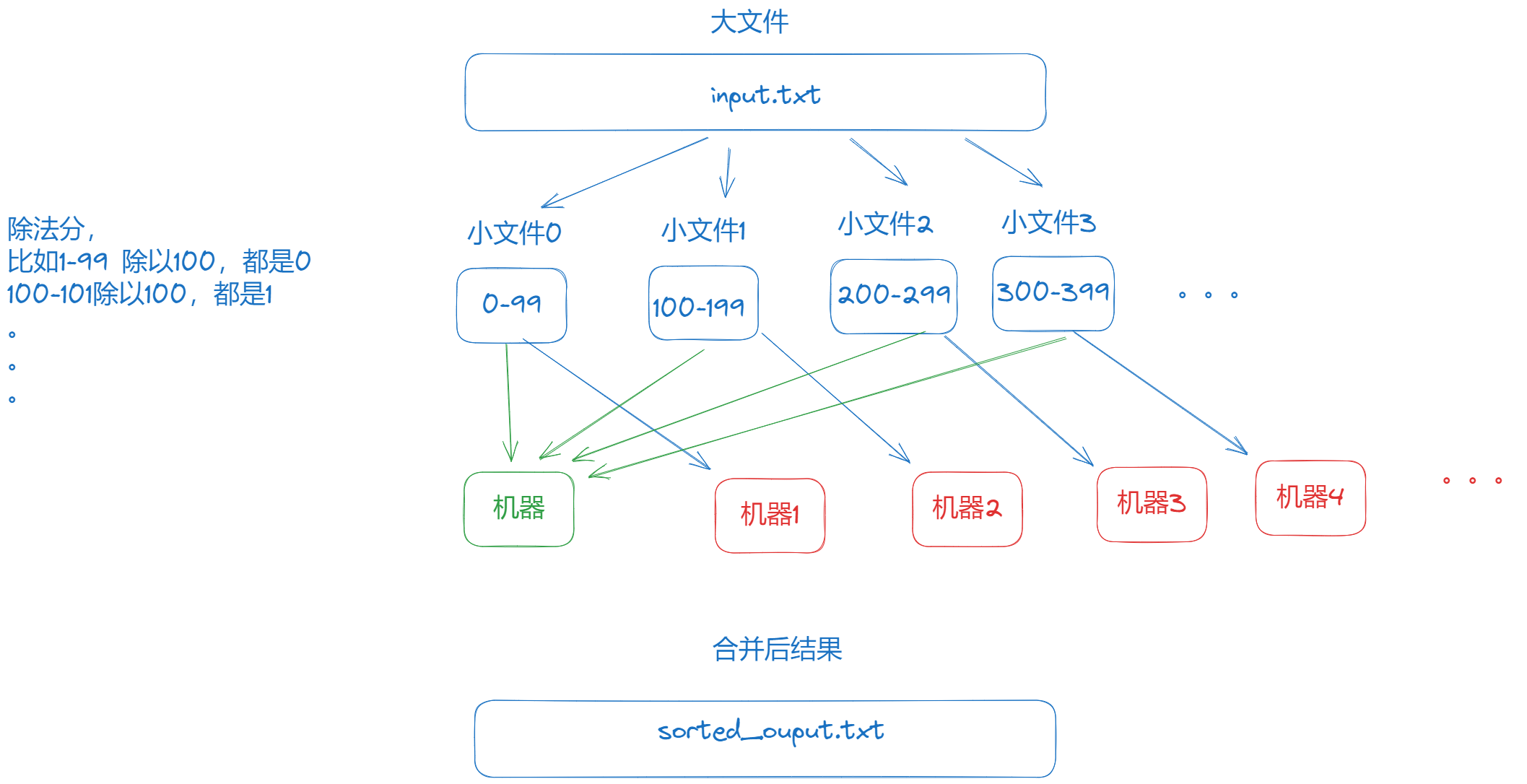
partition process
Results of the run 🔗︎
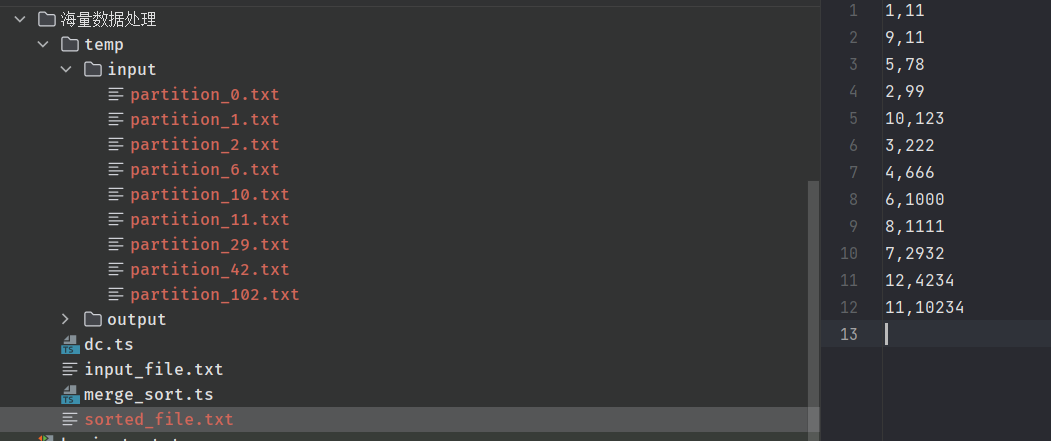
Run Results
temp directory input is the result after splitting into small files, each small file stores the corresponding order data, output is the result after sorting within the small files, and finally sorted_file.txt is the final merged result, which you can see has been sorted.