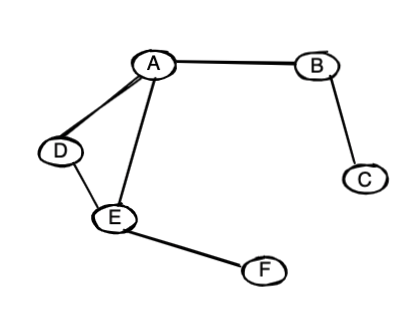
Algorithm Diary #7: Graphs Part 1 - Detect Cycle in an Undirected Graph

/*
  Graph using adjacency list. Support opertaions:
  1 traverse by dfs\bfs
  2 hasCircleByDfs
  3 hasCircleByBfs
  4 hasCircleByDss(Disjoint Set)
  */
class Graph {
  constructor() {
    this.allVertexes = [];
    this.allEdges = [];
    this.adList = new Map();
  }

  addV(v) {
    if (!this.adList.has(v)) {
      this.adList.set(v, []);
    }
    this.allVertexes.push(v);
  }

  addE(source, dest) {
    if (!this.adList.has(source)) {
      this.addV(source);
    }
    if (!this.adList.has(dest)) {
      this.addV(dest);
    }
    this.adList.get(source).push(dest);
    this.adList.get(dest).push(source);
    this.allEdges.push({
      dest,
      source,
    });
  }

  removeV(v) {
    for (let adV of this.adList.get(v)) {
      this.removeE(v, adV);
    }
    this.adList.delete(v);
  }

  removeE(source, dest) {
    this.adList.set(
      source,
      this.adList.get(source).filter((v) => v !== dest)
    );
    this.adList.set(
      dest,
      this.adList.get(dest).filter((v) => v !== source)
    );
  }

  print() {
    for (let v of this.adList.keys()) {
      let cons = "";
      for (let dest of this.adList.get(v)) {
        cons += dest + " ";
      }
      console.log(v + " -> " + cons);
    }
  }

  hasCircleByDss() {
    const dss = new DisjointSet();
    this.allVertexes.forEach((v) => {
      dss.makeSet(v);
    });
    // if  union return true, we find a cycle
    return this.allEdges.some((e) => dss.union(e.source, e.dest));
  }

  bfs(start) {
    const queue = [start];
    const result = [];
    const visited = {};
    visited[start] = true;
    let curV;
    while (queue.length) {
      curV = queue.shift();
      result.push(curV);
      this.adList.get(curV).forEach((dest) => {
        if (!visited[dest]) {
          visited[dest] = true;
          queue.push(dest);
        }
      });
    }
    return result;
  }

  /*
          Key Point: if we find a node is visited, but the node is not the current node's parent
      */
  hasCircleByBfs() {
    const parent = {};
    const result = false;
    const visited = {};
    const queue = [];

    for (let i = 0; i < this.allVertexes.length; i++) {
      const node = this.allVertexes[i];
      if (!visited[node]) {
        visited[node] = true;
        queue.push(node);
        let curV;
        while (queue.length) {
          curV = queue.shift();
          visited[curV] = true;
          const allAdNodes = this.adList.get(curV);
          for (let j = 0; j < allAdNodes.length; j++) {
            const dest = allAdNodes[j];
            if (!visited[dest]) {
              visited[dest] = true;
              parent[dest] = curV;
              queue.push(dest);
            } else if (dest !== parent[curV]) {
              return true;
            }
          }
        }
      }
    }
    return false;
  }

  dfsRecursive(start) {
    const result = [];
    const visited = {};
    const adList = this.adList;
    (function dfs(v) {
      if (!v) return null;
      visited[v] = true;
      result.push(v);
      adList.get(v).forEach((dest) => {
        if (!visited[dest]) {
          return dfs(dest);
        }
      });
    })(start);
    return result;
  }

  dfsIterative(start) {
    const result = [];
    const visited = {};
    const stack = [start];
    let curV;
    visited[start] = true;
    while (stack.length) {
      curV = stack.pop();
      result.push(curV);
      this.adList.get(curV).forEach((dest) => {
        if (!visited[dest]) {
          visited[dest] = true;
          stack.push(dest);
        }
      });
    }
    return result;
  }

  /*
          the key point is: all visited nodes are keep in array, if we repeated push a exsited node, there are more than one path to it(circle exists).
          @params {string} current node
          @params {array} boolean - all visited nodes
          @params {string} parent - current node's parent
      */
  hasCircleUtil(node, visited, parent) {
    // push all nodes to visited
    visited[node] = true;
    const adList = this.adList.get(node) || [];
    for (let i = 0; i < adList.length; i++) {
      // the repeated path, ignore it
      if (adList[i] === parent) continue;
      // we find it is already in the visited queue, we know that. we can reach adList[i] by another path(which means there is a circle)
      if (visited[adList[i]]) return true;
      const hasCycle = this.hasCircleUtil(adList[i], visited, node);
      if (hasCycle) return true;
    }
    return false;
  }
  hasCircleByDfs() {
    const visited = {},
      allV = this.allVertexes;
    // because it is undirected graph, we need to reverse all nodes.
    for (let i = 0; i < allV.length; i++) {
      if (visited[allV[i]]) continue;
      const flag = this.hasCircleUtil(allV[i], visited, null);
      if (flag) return true;
    }
    return false;
  }
}

/*
  three operation: 
  1 makeset
  2 find
  3 union
  */
class DisjointSet {
  constructor() {
    this.map = new Map();
  }
  makeSet(data) {
    this.map.set(data, -1);
  }
  find(x) {
    const parent = this.map.get(x);
    if (parent < 0) {
      return x;
    } else {
      // recurse until you find x's parent
      return this.find(this.map.get(x));
    }
  }
  union(x, y) {
    const xparent = this.find(x);
    const yparent = this.find(y);
    if (xparent !== yparent) {
      // make the represent node's negative plus 1
      this.map.set(xparent, this.map.get(xparent) + this.map.get(yparent));
      // make y point to represents node x
      this.map.set(yparent, xparent);
    } else {
      // same set
      return true;
    }
  }

  console_print() {
    console.log(JSON.stringify(this.map.values()));
  }
}

// test code
const g = new Graph();
var vertices = ["A", "B", "C", "D", "E", "F"];

// adding vertices
for (var i = 0; i < vertices.length; i++) {
  g.addV(vertices[i]);
}

g.addE("A", "B");
g.addE("A", "D");
g.addE("B", "C");
g.addE("D", "E");
g.addE("E", "F");
g.addE("A", "E"); //circle path

g.print();

g.hasCircleByDss("A"); //true
g.hasCircleByDfs();
g.hasCircleByBfs();