数据结构刷题实战
核心直觉 🔗︎
1、迭代法一定会用到while循环,二叉树遍历需要借助stack实现,二分查找只需要借助指针。一般递归更加符合直觉,但是二分查找迭代法更符合直觉。 2、树的前中后序遍历都是递归,不用关心。反而要区分层序遍历和广度遍历,层序遍历不是用递归。 2、
编程工具 🔗︎
Jupyter 是一个vscode插件,方便一次性编译和写作
Array & hash 🔗︎

class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
dict = {}
for num in nums:
if num not in dict:
dict[num] = 1
dict[num] = dict[num] + 1
sorted_items = sorted(dict.items(), key=lambda item: item[1], reverse=True)
#keys = [item[0] for item in sorted_items[:k]]
return sorted_items

# 这个题目是偏算法,但是具体实现的时候会考察到对数组的遍历操作
from typing import List
def productArrayOfSelf(list: List[int]) -> List[int]:
# 1,2,3,4
# prefix: 1 1 2 6
# suffix: 24 12 4 1
n = len(list)
prefix_result = [1] * n
suffix_result = [1] * n
for i in range(n-1):
prefix_result[i+1] = list[i] * prefix_result[i]
for i in reversed(range(1,len(list))):
suffix_result[i-1] = list[i] * suffix_result[i]
result = [1] * n
for i in range(n):
result[i] = prefix_result[i] * suffix_result[i]
return result
productArrayOfSelf([1,2,3,4])
from typing import List
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
prefix_prduct = 1
postfix_product = 1
result = [0] * n
for i in range(n):
result[i] = prefix_prduct
prefix_prduct *= nums[i]
for i in range(n-1, -1, -1):
result[i] *= postfix_product
postfix_product *= nums[i]
return result
print(Solution().productExceptSelf([1,2,3,4])) # 输出: [24, 12, 8, 6]
我们以输入列表 [1,2,3,4] 为例,来详细解释第三步的过程。
在第二步结束后,result 和 postfix_product 的值如下:
- result = [1, 1, 2, 6](存储了每个元素左边所有元素的乘积)
- postfix_product = 1
然后,我们从后向前遍历输入列表 nums:
当 i = 3(对应元素 4)时,我们将 postfix_product 的值(此时为 1)乘到 result[3] 上,得到 result = [1, 1, 2, 6]。然后,我们将 nums[3](即 4)乘到 postfix_product 上,得到 postfix_product = 4。
当 i = 2(对应元素 3)时,我们将 postfix_product 的值(此时为 4)乘到 result[2] 上,得到 result = [1, 1, 8, 6]。然后,我们将 nums[2](即 3)乘到 postfix_product 上,得到 postfix_product = 12。
当 i = 1(对应元素 2)时,我们将 postfix_product 的值(此时为 12)乘到 result[1] 上,得到 result = [1, 12, 8, 6]。然后,我们将 nums[1](即 2)乘到 postfix_product 上,得到 postfix_product = 24。
当 i = 0(对应元素 1)时,我们将 postfix_product 的值(此时为 24)乘到 result[0] 上,得到 result = [24, 12, 8, 6]。
所以,最后返回的结果列表 result 是 [24, 12, 8, 6],其中每个元素都是原始列表中除了自己以外所有元素的乘积。

class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
rows = [{} for _ in range(9)]
columns = [{} for _ in range(9)]
boxes = [{} for _ in range(9)]
for i in range(9):
for j in range(9):
num = board[i][j]
if num != '.':
num = int(num)
box_index = (i // 3 ) * 3 + j // 3
rows[i][num] = rows[i].get(num, 0) + 1
columns[j][num] = columns[j].get(num, 0) + 1
boxes[box_index][num] = boxes[box_index].get(num, 0) + 1
if rows[i][num] > 1 or columns[j][num] > 1 or boxes[box_index][num] > 1:
return False
return True
//模版1: 3*3方格
//notInBox(row - (row % 3), col - (col % 3), board)
function notInBox(startRow, startCol, board) {
let st = new Set();
for (let i = 0; i < 3; i++) {
for (let j = 0; j < 3; j++) {
let cur = board[startRow + i][startCol + j];
if (st.has(cur)) {
return false;
}
if (cur !== ".") {
st.add(cur);
}
}
}
return true;
}
通过行、列、盒子来判断是否存在重复的值。rows是定义成数组,每个数组是一个hash,row[0][5]=0 这种方式计算当前行的5的数量。特别要注意的是盒子的索引:``
(i // 3) * 3 + j // 3 对于任意一个元素,其行索引为i,列索引为j,那么它所在的3x3子数独的索引就可以通过(i // 3 ) * 3 + j // 3计算得到。例如,如果一个元素的行索引为4,列索引为7,那么它所在的3x3子数独的索引就是(4 // 3) * 3 + 7 // 3 = 1 * 3 + 2 = 5,即它在上图中的第5个子数独中。

class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
nums_set = set(nums)
longest = 1
for i in nums_set:
if i - 1 not in nums_set:
current_len = 1
current_num = i + 1
while current_num in nums_set:
current_num += 1
current_len = current_len + 1
longest = max(longest, current_len)
return longest
Solution().longestConsecutive([100, 100,4,200,1,3,2])
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = set()
n, p, z = [], [], []
for i in nums:
if i > 0:
p.append(i)
elif i < 0:
n.append(i)
else:
z.append(i)
N, P = set(n), set(p)
if z:
for i in P:
if -1*i in N:
res.add((-1*i, 0, i))
if len(z) >= 3:
res.add((0,0,0))
for i in range(len(n)):
for j in range(i+1, len(n)):
target = -1*(n[i]+n[j])
if target in P:
res.add(tuple(sorted([n[i], n[j], target])))
for i in range(len(p)):
for j in range(i+1, len(p)):
target = -1*(p[i]+p[j])
if target in N:
res.add(tuple(sorted([p[i],p[j], target])))
return res
在一个一维数组中,找到具有最大和的连续子数组,并返回其最大和。
输入:
arr = [-2, -3, 4, -1, -2, 1, 5, -3]
输出:
7
解释:
最大和的连续子数组为 [4, -1, -2, 1, 5],其和为 4 + (-1) + (-2) + 1 + 5 = 7。
Kadane 算法是一种高效的动态规划算法,用于解决最大子数组和问题。其核心思想是通过遍历数组,动态维护当前子数组的最大和以及全局最大和。
实现代码 🔗︎
function maxSubArraySum(arr: number[]): number {
// 初始化变量
const maxint = Math.pow(2, 53); // JavaScript 中的最大安全整数
let maxSoFar = -maxint - 1; // 全局最大和,初始值设为最小值
let maxEndingHere = 0; // 当前子数组的最大和
// 遍历数组
for (let index = 0; index < arr.length; index++) {
maxEndingHere = maxEndingHere + arr[index]; // 更新当前子数组和
// 如果当前子数组和大于全局最大和,则更新全局最大和
if (maxSoFar < maxEndingHere) {
maxSoFar = maxEndingHere;
}
// 如果当前子数组和小于 0,则重新开始计算子数组
if (maxEndingHere < 0) {
maxEndingHere = 0;
}
}
return maxSoFar; // 返回全局最大和
}
// 测试用例
const arr = [-2, -3, 4, -1, -2, 1, 5, -3];
console.log(maxSubArraySum(arr)); // 输出: 7
初始化:
maxSoFar:记录全局最大和,初始值设为最小值(-Infinity或-Math.pow(2, 53) - 1)。maxEndingHere:记录当前子数组的最大和,初始值为0。
遍历数组:
- 每次将当前元素加入
maxEndingHere,表示扩展当前子数组。 - 如果
maxEndingHere大于maxSoFar,则更新maxSoFar。 - 如果
maxEndingHere小于0,说明当前子数组对后续结果无贡献,重置为0。
- 每次将当前元素加入
返回结果:
- 遍历结束后,
maxSoFar即为最大子数组和。
- 遍历结束后,
- 时间复杂度:
O(n)- 只需遍历数组一次,效率较高。
- 空间复杂度:
O(1)- 只使用了常量级额外空间。
我们有 1TB 的订单数据,需要按照金额大小进行排序。然而,机器内存只有 2GB,无法一次性加载所有数据到内存中。如何解决这个问题?
这是一个典型的 海量数据处理问题,可以利用 分治思想 来解决。分治思想的核心是将一个大问题拆解成多个小问题,分别解决这些小问题后,再将结果合并得到最终答案。
归并排序是分治思想的经典应用。它通过以下步骤实现排序:
- 分解:将数组不断分割,直到每个子数组只剩下一个元素(已排序)。
- 合并:将两个有序数组合并成一个更大的有序数组,最终得到完整的排序结果。
假设我们需要合并两个有序数组 A 和 B:
- 申请一个新数组,大小为
A + B。 - 使用两个游标分别指向
A和B的起始位置。 - 比较两个游标指向的值,将较小的值写入新数组,并移动对应游标。
- 当某个数组的游标到达末尾时,将另一个数组的剩余部分直接复制到新数组。
- 最终将新数组的内容复制回原数组。
以下是归并排序的代码实现:
const mergeSort = (data, p, r) => {
// 如果只剩一个元素,结束递归
if (p >= r) return;
// 分割点
let q = Math.floor((p + r) / 2);
// 分解
mergeSort(data, p, q);
mergeSort(data, q + 1, r);
// 合并
merge(data, p, q, r);
};
const merge = (data, p, q, r) => {
const temp = new Array(r - p + 1);
let i = p;
let j = q + 1;
let k = 0;
// 比较两个数组的元素,按升序写入临时数组
while (i <= q && j <= r) {
if (data[i] <= data[j]) {
temp[k++] = data[i++];
} else {
temp[k++] = data[j++];
}
}
// 将剩余元素写入临时数组
let start = i;
let end = r;
if (j > r) {
end = q;
} else {
start = j;
}
while (start <= end) {
temp[k++] = data[start++];
}
// 将临时数组内容复制回原数组
for (let i = 0; i < r - p + 1; i++) {
data[p + i] = temp[i];
}
return data;
};
export const ms_test_function = () => {
const data = [11, 8, 3, 9, 7, 1, 2, 3];
mergeSort(data, 0, data.length - 1);
return true;
};
回到正题,面对 1TB 订单数据 和 2GB 内存限制,我们可以采用以下步骤解决问题:
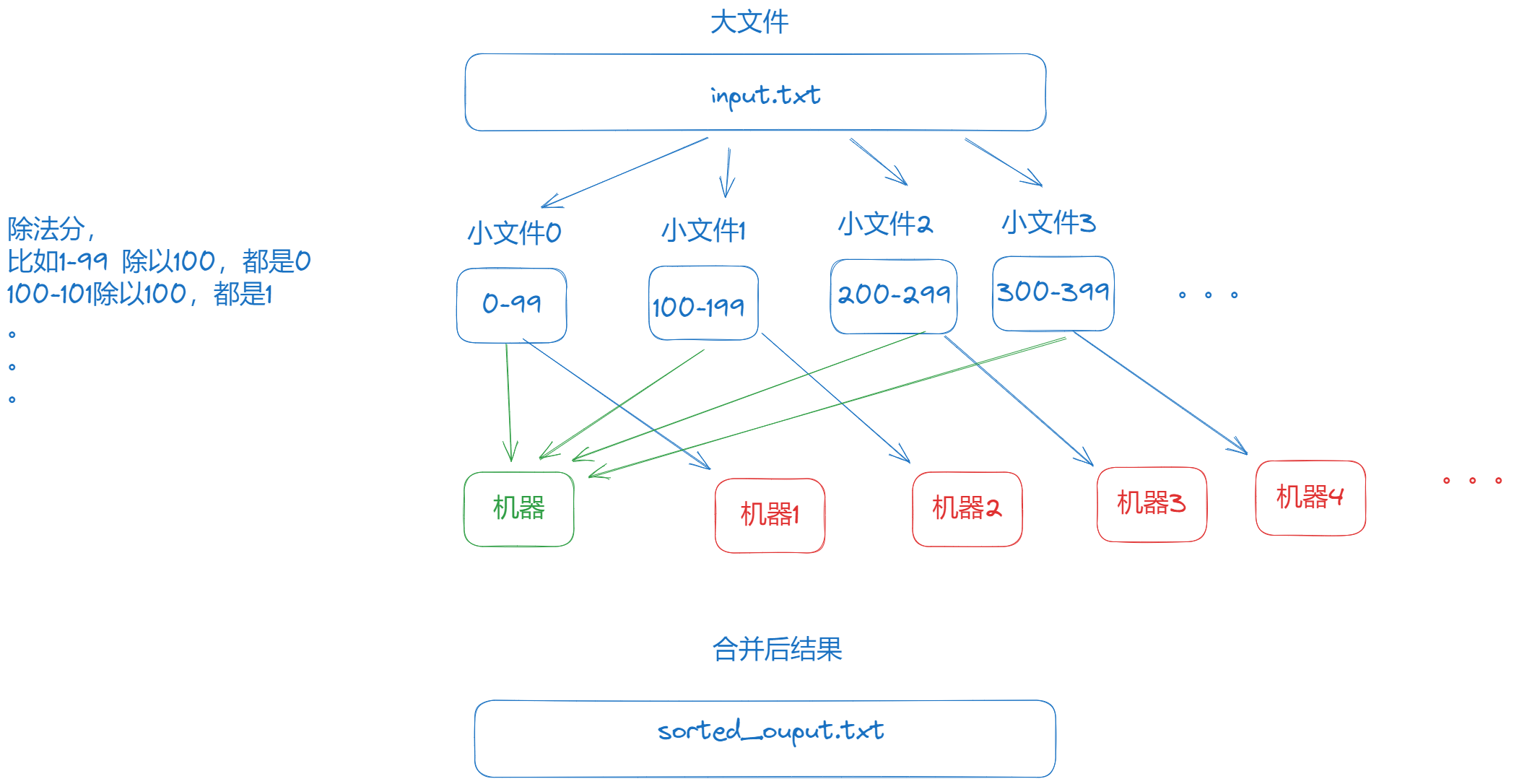
由于内存有限,我们需要将大文件逐行读取并根据订单金额拆分成多个小文件。例如,假设订单金额最大为 1 万,我们可以按照金额范围拆分:
- 0-99 元 → 文件
partition_0.txt - 100-199 元 → 文件
partition_1.txt - 200-299 元 → 文件
partition_2.txt - …
这样做的好处是便于后续合并时,可以根据文件名顺序快速排序。
以下是拆分文件的代码实现:
// Step 1: Divide the file into smaller partitions based on order amounts
function partitionFile(inputFilePath, outputDirPath, callback) {
const partitions = {};
// Read the input file sequentially
const readStream = fs.createReadStream(inputFilePath, { encoding: 'utf8' });
readStream.on('data', (chunk) => {
const orders = chunk.split('\n');
orders.forEach((order) => {
// Extract the order amount from the order entry
const amount = parseFloat(order.split(',')[1]);
// Determine the partition for the order based on its amount
const partition = Math.floor(amount / 100);
// Create a writable stream for the partition file if it doesn't exist
if (!partitions.hasOwnProperty(partition)) {
const partitionFilePath = `${outputDirPath}/partition_${partition}.txt`;
partitions[partition] = fs.createWriteStream(partitionFilePath, { flags: 'a' });
}
// Write the order to the appropriate partition file
partitions[partition].write(`${order}\n`);
});
});
readStream.on('end', () => {
// Close all partition files
for (const partition in partitions) {
partitions[partition].end();
}
callback();
});
}
每个小文件的数据量较小,可以直接加载到内存中进行排序。可以使用高效的排序算法(如归并排序或快速排序),并将排序后的结果写回文件。
以下是排序小文件的代码实现:
// Step 2: Sort each partition individually
function sortPartitions(inputDirPath, outputDirPath, callback) {
fs.readdir(inputDirPath, (err, files) => {
if (err) {
throw err;
}
files.forEach((file) => {
const filePath = `${inputDirPath}/${file}`;
const sortedFilePath = `${outputDirPath}/sorted_${file}`;
// Read the orders from the partition file
const orders = fs.readFileSync(filePath, { encoding: 'utf8' }).split('\n');
// Sort the orders using an efficient algorithm (e.g., merge sort)
const sortedOrders = orders.sort((a, b) => {
const amountA = parseFloat(a.split(',')[1]);
const amountB = parseFloat(b.split(',')[1]);
return amountA - amountB;
});
// Write the sorted orders to the sorted partition file
fs.writeFileSync(sortedFilePath, sortedOrders.join('\n'), { encoding: 'utf8' });
});
callback();
});
}
将所有排序后的小文件按照文件名顺序进行合并。这一步类似于归并排序的合并过程,每次从各个小文件中取出最小的元素,逐步生成最终的排序结果。
以下是合并小文件的代码实现:
// Step 3: Merge the sorted partitions
function mergePartitions(inputDirPath, outputFilePath) {
// Step 1: Perform merge sort on an array of numbers
function mergeSort(arr) {
if (arr.length <= 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
// Step 2: Merge two sorted arrays
function merge(left, right) {
let merged = [];
let i = 0;
let j = 0;
while (i < left.length && j < right.length) {
// 读取文件标题后面的数字
if (parseFloat(left[i].split(',')[1]) <= parseFloat(right[j].split(',')[1])) {
merged.push(left[i]);
i++;
} else {
merged.push(right[j]);
j++;
}
}
while (i < left.length) {
merged.push(left[i]);
i++;
}
while (j < right.length) {
merged.push(right[j]);
j++;
}
return merged;
}
const filePointers = [];
let mergedOutput = '';
fs.readdir(inputDirPath, (err, files) => {
if (err) {
throw err;
}
// Open all sorted partition files and initialize file pointers
files.forEach((file) => {
const filePath = path.join(inputDirPath, file);
const fileData = fs.readFileSync(filePath, 'utf8').trim();
const partitionData = fileData.split('\n');
filePointers.push(partitionData);
});
// Merge the sorted partitions
const sortedOutput = mergeSort(filePointers.flat());
// Format the sorted output
mergedOutput = sortedOutput.join('\n') + '\n';
// Write the merged output to the final sorted file
fs.writeFileSync(outputFilePath, mergedOutput, { encoding: 'utf8' });
});
}
以下是整个流程的运行结果:
- 输入文件:原始 1TB 订单数据。
- 中间文件:
temp/input:分小文件后的结果,每个小文件存储对应的订单数据。temp/output:小文件内部排序后的结果。
- 输出文件:
sorted_file.txt是最终的合并结果,已经按照订单金额排序完成。
假设我们有一个购物车,里面有 n 件商品(价格已知)。我们需要从这 n 件商品中挑选出一些商品,使得它们的总价刚好满足满减要求的价格。例如,满减要求是 10元。
简化后的例子:
- 商品价格数组为
[2, 2, 4, 6, 3] - 满减要求为 10元
目标是从这些商品中选出一些,使得它们的总价尽可能接近满减要求(即 10元),但不超过 3倍满减金额(即 30元)。
这个问题可以类比于经典的 背包问题,即在给定的最大重量限制下,选择物品以最大化总价值。这里的“最大重量”对应于满减金额的上限(如 30元),而“物品的价值”对应于商品的价格。
最直接的解法是通过列出所有可能的商品组合,然后找到满足条件的组合。然而,这种方法的时间复杂度是指数级的(O(2^n)),当商品数量较多时,计算效率会非常低。
我们可以借鉴背包问题的动态规划思想,避免状态的指数级增长。具体来说:
- 使用一个二维状态表
states来记录每一步的状态。 - 每个状态
states[i][j]表示前i件商品能否凑出总价为j的组合。 - 通过状态转移方程,逐步推导出最终结果。
状态定义:
states[i][j]:表示前i件商品是否能凑出总价为j的组合。- 初始状态:
states[0][0] = true(不选任何商品时,总价为 0 是可行的)。 - 如果第
i件商品的价格items[i]小于等于当前总价j,则可以通过选择或不选择该商品来更新状态。
状态转移方程:
- 不选择第
i件商品:- 如果
states[i-1][j] = true,则states[i][j] = true。
- 如果
- 选择第
i件商品:- 如果
states[i-1][j-items[i]] = true,则states[i][j] = true。
- 如果
边界条件:
- 总价不能超过 3倍满减金额(即
3 * w)。 - 如果找不到满足条件的组合,则返回空结果。
以下是基于上述思路的 JavaScript 实现:
/**
* 双11凑单问题
* @param {number[]} items 商品价格数组
* @param {number} n 商品个数
* @param {number} w 凑单金额
*/
function double11advance(items, n, w) {
// 初始化状态表
let states = new Array(n);
for (let i = 0; i < n; i++) {
states[i] = new Array(3 * w + 1).fill(false);
}
// 初始状态
states[0][0] = true; // 不选第一个商品
if (items[0] <= 3 * w) {
states[0][items[0]] = true; // 选第一个商品
}
// 动态规划填表
for (let i = 1; i < n; i++) {
// 不选择第 i 件商品
for (let j = 0; j <= 3 * w; j++) {
if (states[i - 1][j] === true) {
states[i][j] = states[i - 1][j];
}
}
// 选择第 i 件商品
for (let j = 0; j <= 3 * w - items[i]; j++) {
if (states[i - 1][j] === true) {
states[i][j + items[i]] = true;
}
}
}
// 找到最接近满减金额的总价
let j;
for (j = w; j < 3 * w + 1; j++) {
if (states[n - 1][j] === true) {
break;
}
}
// 如果找不到满足条件的组合
if (j === 3 * w + 1) {
console.log("无法找到满足条件的商品组合");
return;
}
// 回溯找出具体选择了哪些商品
for (let i = n - 1; i >= 1; i--) {
if (j - items[i] >= 0 && states[i - 1][j - items[i]] === true) {
console.log(items[i]); // 打印已选商品
j -= items[i];
}
}
// 检查是否选择了第 0 件商品
if (j !== 0) {
console.log(items[0]);
}
}
输入
const items = [2, 2, 4, 6, 3];
const n = items.length;
const w = 10;
double11advance(items, n, w);
输出
6
4
解释:选择价格为 6 和 4 的商品,总价为 10,刚好满足满减要求。
- 时间复杂度:
- 填表过程需要遍历每个商品和每个可能的总价,时间复杂度为 O(n * 3w),其中
n是商品数量,w是满减金额。
- 填表过程需要遍历每个商品和每个可能的总价,时间复杂度为 O(n * 3w),其中
- 空间复杂度:
- 使用了一个二维数组
states,空间复杂度为 O(n * 3w)。
- 使用了一个二维数组
在自然语言处理、文本匹配等领域,我们经常需要量化两个字符串的相似度。一个常用的指标是 编辑距离(Edit Distance),它表示将一个字符串转换为另一个字符串所需的最小编辑操作次数。编辑操作包括:
- 插入:在字符串中插入一个字符。
- 删除:从字符串中删除一个字符。
- 替换:将字符串中的某个字符替换为另一个字符。
编辑距离越小,说明两个字符串越相似。
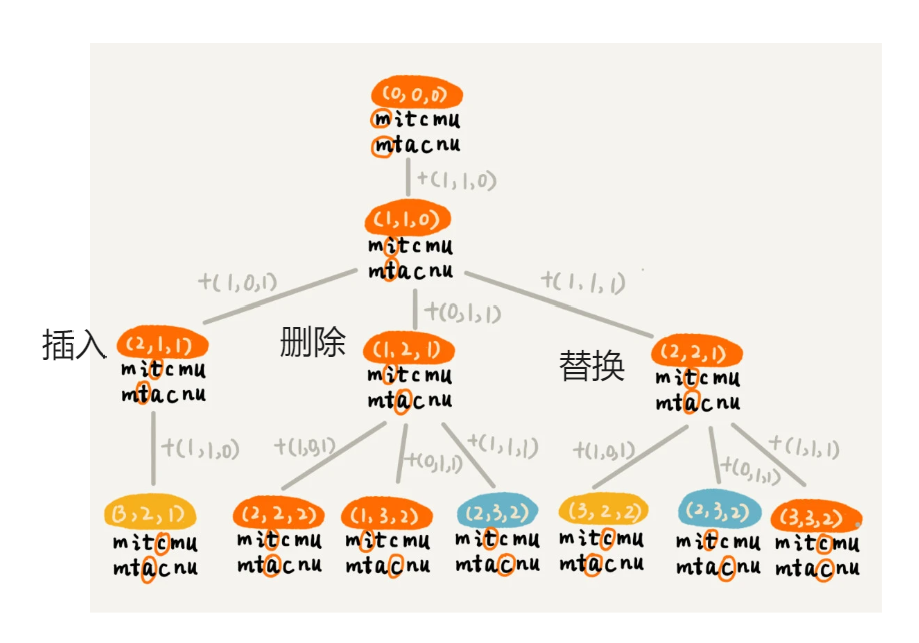
给定两个字符串 mitcmu 和 mtacnu,它们的编辑距离是多少?
一种直观的解决方法是通过回溯算法,枚举所有可能的操作序列,找到最小的编辑距离。具体步骤如下:
- 如果
a[i] == b[j],则无需操作,递归考察a[i+1]和b[j+1]。 - 如果
a[i] != b[j],可以进行以下操作之一:- 删除:删除
a[i]或b[j],然后递归考察剩余部分。 - 插入:在
a[i]前插入与b[j]相同的字符,或在b[j]前插入与a[i]相同的字符。 - 替换:将
a[i]替换为b[j]或将b[j]替换为a[i]。
- 删除:删除
这种方法的时间复杂度较高,因为会重复计算相同的子问题。
为了避免重复计算,我们可以使用动态规划来优化回溯算法。定义状态 minDist[i][j] 表示将字符串 a[0...i-1] 转换为字符串 b[0...j-1] 所需的最小编辑距离。
状态转移方程
- 如果
a[i-1] == b[j-1],则无需操作: [ minDist[i][j] = minDist[i-1][j-1] ] - 如果
a[i-1] != b[j-1],可以选择以下三种操作之一:- 插入:
minDist[i][j] = minDist[i][j-1] + 1 - 删除:
minDist[i][j] = minDist[i-1][j] + 1 - 替换:
minDist[i][j] = minDist[i-1][j-1] + 1
- 插入:
综合上述两种情况,状态转移方程为: [ minDist[i][j] = \begin{cases} minDist[i-1][j-1], & \text{if } a[i-1] == b[j-1] \ \min(minDist[i-1][j]+1, minDist[i][j-1]+1, minDist[i-1][j-1]+1), & \text{if } a[i-1] \neq b[j-1] \end{cases} ]
初始条件:
- 将空字符串转换为目标字符串时,编辑距离等于目标字符串的长度: [ minDist[i][0] = i \quad (i = 0, 1, …, n) ] [ minDist[0][j] = j \quad (j = 0, 1, …, m) ]
以下是基于动态规划的 JavaScript 实现:
/**
* 计算两个字符串的编辑距离
* @param {string} a 字符串A
* @param {number} n 字符串A的长度
* @param {string} b 字符串B
* @param {number} m 字符串B的长度
* @returns {number} 最小编辑距离
*/
function lwstDP(a, n, b, m) {
// 初始化二维数组 minDist
const minDist = new Array(n + 1);
for (let i = 0; i < n + 1; i++) {
minDist[i] = new Array(m + 1);
minDist[i][0] = i; // 将空字符串转换为a[0...i-1]的编辑距离
}
for (let j = 0; j < m + 1; j++) {
minDist[0][j] = j; // 将空字符串转换为b[0...j-1]的编辑距离
}
// 动态规划填表
for (let i = 1; i < n + 1; i++) {
for (let j = 1; j < m + 1; j++) {
if (a[i - 1] === b[j - 1]) {
// 字符相等,无需操作
minDist[i][j] = minOfThree(
minDist[i - 1][j] + 1, // 删除
minDist[i][j - 1] + 1, // 插入
minDist[i - 1][j - 1] // 不操作
);
} else {
// 字符不等,取最小操作
minDist[i][j] = minOfThree(
minDist[i - 1][j] + 1, // 删除
minDist[i][j - 1] + 1, // 插入
minDist[i - 1][j - 1] + 1 // 替换
);
}
}
}
return minDist[n][m]; // 返回最终结果
}
/**
* 辅助函数:返回三个数中的最小值
* @param {number} n1 第一个数
* @param {number} n2 第二个数
* @param {number} n3 第三个数
* @returns {number} 最小值
*/
function minOfThree(n1, n2, n3) {
return Math.min(n1, Math.min(n2, n3));
}
输入
const a = "mitcmu";
const b = "mtacnu";
const n = a.length;
const m = b.length;
console.log(lwstDP(a, n, b, m)); // 输出:3
输出
3
将 mitcmu 转换为 mtacnu 的最小编辑距离为 3,可以通过以下操作实现:
替换
i为t。替换
c为a。替换
m为n。时间复杂度:
- 动态规划表的大小为
(n+1) x (m+1),每个状态的计算时间为 O(1)。 - 总时间复杂度为 O(n * m),其中
n和m分别为两个字符串的长度。
- 动态规划表的大小为
空间复杂度:
- 使用了一个二维数组
minDist,空间复杂度为 O(n * m)。
- 使用了一个二维数组
给定一个整数数组,其中每个元素表示从该位置可以向前跳的最大步数。编写一个函数返回到达数组末尾所需的最小跳跃次数。如果某个元素为 0,则无法通过该元素。如果无法到达终点,则返回 -1。
输入:
arr[] = {1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9}
输出:
3
解释:
- 第 1 次跳跃:从索引
0跳到索引1(因为arr[0] = 1)。 - 第 2 次跳跃:从索引
1跳到索引4(因为arr[1] = 3,可以选择跳到索引2、3或4)。 - 第 3 次跳跃:从索引
4跳到索引10(因为arr[4] = 9,直接跳到终点)。
输入:
arr[] = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
输出:
10
解释:每次只能跳一步,因此需要 10 次跳跃才能到达终点。
贪心算法(优化版暴力解法)
function miniJumpsToEnd(arr) {
const n = arr.length;
// 如果数组长度为 1 或更小,无需跳跃
if (n <= 1) return 0;
// 如果起点为 0 且数组长度大于 1,无法跳跃
if (arr[0] == 0) return -1;
let maxReach = arr[0]; // 当前能够到达的最远索引
let step = arr[0]; // 当前剩余的步数
let jumps = 1; // 总跳跃次数
for (let i = 1; i < n; i++) {
// 如果当前索引已经到达或超过终点
if (i == n - 1) {
return jumps;
}
// 更新能够到达的最远索引
maxReach = Math.max(maxReach, i + arr[i]);
// 消耗一步
step--;
// 如果当前剩余步数为 0,需要进行一次跳跃
if (step == 0) {
jumps++;
// 如果当前索引已经超过最大可达范围,说明无法到达终点
if (i >= maxReach) {
return -1;
}
// 更新剩余步数为新的最大可达范围减去当前索引
step = maxReach - i;
}
}
return -1; // 如果循环结束仍未返回结果,说明无法到达终点
}
核心思想
使用贪心算法动态维护三个变量:maxReach:记录当前能够到达的最远索引。step:记录当前剩余的步数。jumps:记录总的跳跃次数。
流程
- 遍历数组时,更新
maxReach为当前索引加上当前元素值的最大值。 - 每次消耗一步(
step--),当step为0时,表示需要进行一次跳跃,并更新剩余步数。 - 如果当前索引超过了
maxReach,说明无法继续前进,返回-1。
- 遍历数组时,更新
边界条件
- 如果数组长度为
1,直接返回0。 - 如果起点为
0且数组长度大于1,直接返回-1。
- 如果数组长度为
时间复杂度:
只需遍历数组一次,因此时间复杂度为 O(n)。空间复杂度:
只使用了常量级额外空间,因此空间复杂度为 O(1)。
输入:
arr[] = {1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9}
执行过程:
- 初始状态:
maxReach = 1,step = 1,jumps = 1 - 遍历到索引
1:更新maxReach = 4, 消耗step,进行第 2 次跳跃。 - 遍历到索引
4:更新maxReach = 13, 消耗step,进行第 3 次跳跃。 - 到达终点,返回
3。
输出:
3
输入:
arr[] = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
执行过程:
- 每次只能跳一步,总共需要 10 次跳跃。
输出:
10
Two Pointer 🔗︎
Valid Palindrome ![[Pasted image 20240225105519.png]]
class Solution:
def isPalindrome(self, s: str) -> bool:
start = 0
end = len(s) - 1
while start < end:
if not s[start].isalnum():
start += 1
continue
if not s[end].isalnum():
end -= 1
continue
if s[start].lower() != s[end].lower():
return False
start += 1
end -= 1
return True
Two Sum II Input Array Is Sorted

class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
start = 0
end = len(numbers) - 1
while start < end:
sum = numbers[start] + numbers[end]
if sum == target:
return [start, end]
elif sum < target:
start += 1
else:
end -= 1
return []
Container With Most Water (Hard)

# min(LMin, RMax) - h(i)
class Solution:
def maxArea(self, height: List[int]) -> int:
n = len(height)
l, r = 0, n - 1
ans = 0
while l <= r:
ans = max(ans, (r-l)*min(height[l], height[r]))
if height[l] < height[r]: l += 1
else: r -= 1
return ans
hint:如果移动高的指针,宽度变小,而高度不变,水位不会变多

# min(LMin, RMax) - h(i)
class Solution:
def maxArea(self, height: List[int]) -> int:
if not height:
return 0
l, r = 0, len(height) - 1
lMax, rMax = height[0], height[-1]
res = 0
while l < r:
if lMax < rMax:
l += 1
lMax = max(lMax, height[l])
res += lMax - height[l]
else:
r -= 1
rMax = max(rMax, height[r])
res += rMax - height[r]
return res
给定一个字符串,找到其中最长的回文子串。
输入:
"forgeeksskeegfor"
输出:
"geeksskeeg"
输入:
"Geeks"
输出:
"ee"
要找到字符串中的最长回文子串,可以采用中心扩展法。具体步骤如下:
- 遍历字符串的每个字符,将其视为回文中心。
- 向左右两侧扩展,检查是否满足回文条件(即左右字符相等)。
- 跳过重复字符以处理偶数长度的回文。
- 记录当前最长回文子串的起始位置和长度,并在遍历结束后返回结果。
以下是基于 TypeScript 的代码实现:
function longestPalindrome(str: string): string {
const n = str.length;
if (n === 0) return "";
let maxLength = 1; // 最长回文子串的长度
let start = 0; // 最长回文子串的起始位置
for (let index = 0; index < n; index++) {
let low = index - 1;
let high = index + 1;
// 跳过右侧重复字符
while (high < n && str[high] === str[index]) {
high++;
}
// 跳过左侧重复字符
while (low >= 0 && str[low] === str[index]) {
low--;
}
// 中间部分是回文,继续向外扩展
while (low >= 0 && high < n && str[low] === str[high]) {
low--;
high++;
}
// 计算当前回文子串的长度
const length = high - low - 1;
if (maxLength < length) {
maxLength = length;
start = low + 1;
}
}
// 返回最长回文子串
return str.substring(start, start + maxLength);
}
O(n²):
- 外层循环遍历整个字符串,时间复杂度为 O(n)。
- 内层循环从每个字符为中心向两侧扩展,最坏情况下会扩展到头尾,时间复杂度为 O(n)。
- 因此,总时间复杂度为 O(n²)。
O(1):
- 只使用了常量级别的额外空间(如
low、high、maxLength等变量),因此空间复杂度为 O(1)。
- 只使用了常量级别的额外空间(如
Stack 🔗︎

class Solution:
def isValid(self, s: str) -> bool:
stack = list()
dict = { "(": ")", "{": "}", "[": "]" }
for char in s:
if len(stack) > 0 and stack[-1] not in dict:
return False
if len(stack) == 0 or dict[stack[-1]] != char:
stack.append(char)
continue
stack.pop()
return len(stack) == 0

class MinStack:
def __init__(self):
self.list = []
self.min = []
def push(self, val: int) -> None:
self.list.append(val)
self.min.append(val if not self.min else min(val, self.min[-1]))
def pop(self) -> None:
self.list.pop()
self.min.pop()
def top(self) -> int:
return self.list[-1]
def getMin(self) -> int:
return self.min[-1]
Evaluate Reverse Polish Notation

class Solution:
def evalRPN(self, tokens: List[str]) -> int:
stack = []
ops = ['+', '-', '*', '/']
for token in tokens:
if token in ops:
a = stack.pop()
b = stack.pop()
if token == '+':
result = int(b) + int(a)
elif token == '*':
result = int(b) * int(a)
elif token == '/':
result = int(b) / int(a)
else:
result = int(b) - int(a)
stack.append(int(result))
continue
stack.append(int(token))
return stack[-1]

# 单调递减堆栈存储信息
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
stack = [] # pair: temp, index
res = [0] * len(temperatures)
for i, v in enumerate(temperatures):
while stack and v > stack[-1][0]:
stackT, stackIndex = stack.pop()
res[stackIndex] = (i - stackIndex)
stack.append([v, i])
return res
给定一个数组和一个整数 K,找到每个长度为 K 的连续子数组的最大值。
输入:
arr[] = {1, 2, 3, 1, 4, 5, 2, 3, 6}, K = 3
输出:
3 3 4 5 5 5 6
解释:
- 子数组
[1, 2, 3]的最大值是3 - 子数组
[2, 3, 1]的最大值是3 - 子数组
[3, 1, 4]的最大值是4 - 子数组
[1, 4, 5]的最大值是5 - 子数组
[4, 5, 2]的最大值是5 - 子数组
[5, 2, 3]的最大值是5 - 子数组
[2, 3, 6]的最大值是6
方法 1:暴力解法
实现代码 🔗︎
function getMaxK(arr, k) {
if (!arr) return;
if (arr.length <= k) {
return Math.max(...arr);
}
for (let index = 0; index <= arr.length - k; index++) {
let result = Math.max(arr[index], arr[index + 1], arr[index + 2]);
console.log(result + " ");
}
}
- 时间复杂度:
外层循环遍历(n-k)次,内层计算最大值需要k次操作,因此总时间复杂度为 O(n*k)。 - 空间复杂度:
不需要额外空间,因此空间复杂度为 O(1)。
方法 2:AVL 树
AVL 树是一种高度平衡的二叉搜索树(BST),其左右子树的高度差不超过 1。它支持插入、删除和查找操作的时间复杂度均为 O(log k),非常适合用于动态维护最值。
实现代码
function getMaxK(arr, k) {
const res = [];
const queue = [];
let index = 0;
// 初始化前 k 个元素
for (; index < k; index++) {
queue.push(arr[index]);
}
queue.sort((a, b) => b - a); // 排序以模拟 AVL 树
res.push(queue[0]);
// 滑动窗口处理剩余元素
for (; index < arr.length; index++) {
const element = arr[index];
queue.push(element);
queue.sort((a, b) => b - a); // 插入后重新排序
res.push(queue[0]);
queue.splice(arr[index - k + 1], 1); // 删除滑出窗口的元素
}
return res;
}
- 时间复杂度:
遍历数组需要n次操作,每次插入或删除元素需要log k时间,因此总时间复杂度为 O(n*log k)。 - 空间复杂度:
维护一个大小为k的队列,因此空间复杂度为 O(k)。
构建 AVL 树的关键模板
节点平衡模板
const balance = this.getBalance(node); // 左左情况 if (balance > 1 && data < node.left.data) { return this.rightRotate(node); } // 右右情况 if (balance < -1 && data > node.right.data) { return this.leftRotate(node); } // 左右情况 if (balance > 1 && data > node.left.data) { node.left = this.leftRotate(node.left); return this.rightRotate(node); } // 右左情况 if (balance < -1 && data < node.right.data) { node.right = this.rightRotate(node.right); return this.leftRotate(node); }左旋模板
function leftRotate(x) { let y = x.right; let T2 = y.left; y.left = x; x.right = T2; x.height = Math.max(height(x.left), height(x.right)) + 1; y.height = Math.max(height(y.left), height(y.right)) + 1; return y; }右旋模板
function rightRotate(y) { let x = y.left; let T2 = x.right; x.right = y; y.left = T2; y.height = Math.max(height(y.left), height(y.right)) + 1; x.height = Math.max(height(x.left), height(x.right)) + 1; return x; }
方法 3:双栈法
实现代码
const s1 = []; // 滑动窗口
const s2 = []; // 临时窗口
const n = arr.length;
// 初始化
for (let index = 0; index < k - 1; index++) {
insert(s2, arr[index]);
}
for (let i = 0; i <= n - k; i++) {
// 更新窗口
if (i - 1 >= 0) update(s1, s2);
// 插入新元素
insert(s2, arr[i + k - 1]);
// 记录最大值
res.push(Math.max(s1[s1.length - 1].max, s2[s2.length - 1].max));
}
分析
- 时间复杂度:
每个元素最多被插入和删除一次,因此总时间复杂度为 O(n)。 - 空间复杂度:
使用两个栈存储最多k个元素,因此空间复杂度为 O(k)。
方法 4:大顶堆(Max-Heap)
使用大顶堆动态维护当前窗口中的最大值。大顶堆的特点是可以快速获取最大值,并支持高效的插入和删除操作。
1、分析
- 时间复杂度:
每次插入和删除操作的时间复杂度为 O(log k),总时间复杂度为 O(n*log k)。 - 空间复杂度:
堆中最多存储k个元素,因此空间复杂度为 O(k)。
总结 🔗︎
| 方法 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 暴力解法 | O(n*k) | O(1) | 数据规模较小 |
| AVL 树 | O(n*log k) | O(k) | 动态维护最值,数据规模较大 |
| 双栈法 | O(n) | O(k) | 高效且易于实现 |
| 大顶堆 | O(n*log k) | O(k) | 动态维护最值,适合大规模数据 |
根据实际需求选择合适的算法。如果对性能要求较高且数据规模较大,推荐使用 双栈法 或 大顶堆。
Binary Search 🔗︎
思维误区
1、二分查找不是单纯找指定元素。它本质上可以**缩短范围**,只要你找到条件。这里比较的是当前行的最小和最大的元素,而不是两行的第一个元素。
2、迭代法和递归都是可以实现二分查找的
class Solution:
def search(self, nums: List[int], target: int) -> int:
def bs(low, high):
if low > high:
return -1
mid = low + (high - low) // 2
if nums[mid] < target:
return bs(mid + 1, high)
elif nums[mid] > target:
return bs(low, mid - 1)
else:
return mid
return bs(0, len(nums) - 1)
# 通过指针直接操作,不需要额外的数组存储
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
rows, cols = len(matrix), len(matrix[0])
top, bot = 0, rows - 1
targetRow = -1
while top <= bot: # = 表示获取最后一个值
mid = bot + (top - bot) // 2
if target > matrix[mid][-1]:
top = mid + 1
elif target < matrix[mid][0]:
bot = mid - 1
else:
targetRow = mid
break # 找到当前行
l, r = 0, cols - 1
while l <= r:
m = l + (r - l) // 2
if target > matrix[row][m]:
l = m + 1
elif target < matrix[row][m]:
r = m - 1
else:
return True

class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
l, r = 1, max(piles)
res = r
while l <= r:
k = l + (r - l) // 2
hours = 0
for p in piles:
hours += math.ceil(p / k)
if hours <= h:
res = min(res, k)
r = k - 1
else:
l = k + 1
return res
Find Minimum In Rotated Sorted Array
查找旋转排序数组中的最小值

class Solution:
def findMin(self, nums: List[int]) -> int:
res = nums[0]
l, r = 0, len(nums) - 1
while l <= r:
if nums[l] < nums[r]:
res = min(res, nums[l])
break
m = l + (r - l) // 2
res = min(res, nums[m])
if nums[m] >= nums[l]:
l = m + 1
else:
r = m - 1
return res
Search In Rotated Sorted Array 在旋转排序数组中搜索

# 2 3 4 0 1 left sorted
# 3 4 0 1 2 right sorted
class Solution:
def search(self, nums: List[int], target: int) -> int:
l, r = 0, len(nums) - 1
while l <= r:
mid = l + (r - l) // 2
if nums[mid] == target:
return mid
# left sorted portion
if nums[l] <= nums[mid]:
if target > nums[mid] or target < nums[l]:
l = mid + 1
else:
r = mid - 1
# right sorted portion
else:
if target < nums[mid] or target > nums[r]:
r = mid - 1
else:
l = mid + 1
return -1
Time Based Key Value Store 基于时间的键值存储

class TimeMap:
def __init__(self):
self.dict = {} # key: list of [value, timestamp]
def set(self, key: str, value: str, timestamp: int) -> None:
# already sorted
if key not in self.dict:
self.dict[key] = []
self.dict[key].append([value, timestamp])
def get(self, key: str, timestamp: int) -> str:
values = self.dict.get(key, [])
# find in binary search
l, r = 0, len(values) - 1
while l <= r: # equal to get last value
mid = l + (r - l) // 2
if values[mid][1] <= timestamp:
# 查找最后一个小于等于给定值的元素
if (mid == len(values) - 1) or values[mid + 1][1] > timestamp:
return values[mid][0]
else:
l = mid + 1
else:
r = mid - 1
return ''
Sliding Window 🔗︎
Best Time to Buy And Sell Stock 买卖股票的最佳时机

class Solution:
def maxProfit(self, prices: List[int]) -> int:
l, r = 0, 1
maxP = 0
while r < len(prices):
if prices[l] < prices[r]:
profit = prices[r] - prices[l]
maxP = max(maxP, profit)
else:
l = r
r += 1
return maxP
最长非重复子字符串。 比如abcabcddd 输出 abc
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
charSet = set()
l = 0
res = 0
for r in range(len(s)):
# 如果a已存在,则从左边移除 因为我们是要找到非重复子字符串
while s[r] in charSet:
charSet.remove(s[l])
l += 1
charSet.add(s[r])
res = max(res, r - l + 1)
return res
Longest Repeating Character Replacement 最长重复字符替换

class Solution:
def characterReplacement(self, s: str, k: int) -> int:
count = {}
res = 0
l = 0
for r in range(len(s)):
# add count of right char
count[s[r]] = 1 + count.get(s[r], 0)
# not effective window
while (r - l + 1) - max(count.values()) > k:
count[s[l]] -= 1 # add count of left char
l += 1 # move the left cursor
# effective window res = max(res, r - l + 1)
return res

# 寻找字符游戏,不关心顺序。
# 最简单:遍历两个数组,逐个对比,复杂度是n*m
# 优化:因为字符只有26个,可以建立一个hashmap,滑动窗口移动时,判断是否hashmap中存在,然后和数组a比较是否相等。复杂度是n
class Solution:
def checkInclusion(self, s1: str, s2: str) -> bool:
if len(s1) > len(s2): return False
# 初始化hashmap
s1Count, s2Count = [0] * 26, [0]*26
# 统计初始的出现次数
for i in range(len(s1)):
s1Count[ord(s1[i]) - ord('a')] += 1 # 统计出现次数
s2Count[ord(s2[i]) - ord('a')] += 1
# 如果找到匹配的应该是26,因为初始化其他的都是0
# 统计初始的匹配次数
matches = 0
for i in range(26):
matches += (1 if s1Count[i] == s2Count[i] else 0)
# 滑动窗口往右移动1位
l = 0
for r in range(len(s1), len(s2)): # 参数2是结束索引
if matches == 26: return True # 找到匹配字符
# 增加右邊字符判斷匹配情況
index = ord(s2[r]) - ord('a')
s2Count[index] += 1 # 匹配次數加1
if s1Count[index] == s2Count[index]:
matches += 1
elif s1Count[index] + 1 == s2Count[index]: # 因爲s2Count加了1,所以s1Count要+1進行比較
matches -= 1
# 移除左邊字符,計算匹配情況
index = ord(s2[l]) - ord('a')
s2Count[index] -= 1 # 匹配次數減1
if s1Count[index] == s2Count[index]:
matches += 1
elif s1Count[index] - 1 == s2Count[index]: # 應爲s2Count減了1,所以s1也要減1后比較
matches -= 1
l += 1 # 左邊指針移動
return matches == 26
简易版本
# 滑动窗口指针只有i,
# The only thing we care about any particular substring in `s2` is having the same number of characters as in the `s1`. So we create a hashmap with the count of every character in the string `s1`. Then we slide a window over the string `s2` and decrease the counter for characters that occurred in the window. As soon as all counters in the hashmap get to zero that means we encountered the permutation.
class Solution:
def checkInclusion(self, s1: str, s2: str) -> bool:
def checkInclusion(self, s1: str, s2: str) -> bool:
# 初始不匹配都为1
cntr, w = Counter(s1), len(s1)
for i in range(len(s2)):
# 1 表示不匹配 0 表示匹配
if s2[i] in cntr: # 右边指针找到匹配 减1
cntr[s2[i]] -= 1
if i >= w and s2[i - w] in cntr: # 左边指针移出滑动窗口,不匹配加1
cntr[s2[i - w]] += 1
# 最后都为0说明找到匹配
if all([cntr[i] == 0 for i in cntr]):
return True
return False
def test(s1, s2):
s1_count = [0] * 26
s2_count = [0] * 26
len1 = len(s1)
len2 = len(s2)
if len1 > len2:
return False
'''
s1: ab
s2: aefbaad
s1_count:
{
1: 2, 'a'
2: 1, 'b'
}
s2_count:
{
1: 2, 'a'
8: 1, 'e'
}
'''
for i in range(len1):
s1_count[ord(s1[i]) - ord('a')] += 1
s2_count[ord(s2[i]) - ord('a')] += 1
for i in range(len2 - len1): # 滑动距离0-4
if s1_count == s2_count: # 如果统计出来次数一样 就说明是子串
return True
# 移动窗口长度
s2_count[ord(s2[i]) - ord('a')] -= 1 # 移除最左边的字符 数量-1
s2_count[ord(s2[i + len1] - ord('a'))] += 1 # 添加右边的1个字符
# 这个最后判断一下 ad
return s1_count == s2_count
LinkedList 🔗︎

错误的做法:
1、一次操作移动两个指针
2、写法是错误的 curr.next = curr
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# 双指针法
# None <- a <- b 前面有一个None哨兵指针
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
prev, curr = None, head
while curr: # 每次循环只修改一次指针
next = curr.next # 保存之前的指针,避免指针断开
# 修改指针 curr.next = curr 这种写法是错误的
curr.next = prev
# 指针往前移动
prev = curr
curr = next
return prev
Merge Two Sorted Lists 合并两个排序列表

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
dummy = ListNode()
tail = dummy
while list1 and list2:
if list1.val < list2.val:
tail.next = list1
list1 = list1.next
else:
tail.next = list2
list2 = list2.next
tail = tail.next
if list1:
tail.next = list1
else:
tail.next = list2
return dummy.next
# slow, fast pointer and dummy node
class Solution:
def reorderList(self, head: Optional[ListNode]) -> None:
class Solution:
def reorderList(self, head: Optional[ListNode]) -> None:
# find middle
slow, fast = head, head.next
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# reverse second half
second = slow.next
prev = slow.next = None
while second:
tmp = second.next
second.next = prev
prev = second
second = tmp
# merge tow half
first, second = head, prev
while second:
tmp1, tmp2 = first.next, second.next
first.next = second
second.next = tmp1
first, second = tmp1, tmp2
Remove Nth Node From End of List 从列表末尾删除第 n 个节点

错误示范:
1、快慢指针不是说一定要同时移动的,可以一个先不动,fast指针先移动到指定位置
# slow, fast pointer and dummy node
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dummy = ListNode(0, head)
left = dummy
right = head
while n > 0 and right:
right = right.next
n -= 1
while right:
left = left.next
right = right.next
# delete
left.next = left.next.next
return dummy.next
Copy List With Random Pointer 使用随机指针复制列表

# 通过先创建节点,再连线(创建hashmap建立两个链表的联系)
class Solution:
def copyRandomList(self, head: 'Optional[Node]') -> 'Optional[Node]':
oldToCopy = { None : None }
# one pass
cur = head
while cur:
copy = Node(cur.val)
oldToCopy[cur] = copy
cur = cur.next
# two pass
cur = head
while cur:
copy = oldToCopy[cur]
copy.next = oldToCopy[cur.next]
copy.random = oldToCopy[cur.random]
cur = cur.next
return oldToCopy[head]
# 考虑 7 + 8 这样的边界case
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
dummy = ListNode()
cur = dummy
carry = 0
while l1 or l2 or carry:
v1 = l1.val if l1 else 0
v2 = l2.val if l2 else 0
# new digit
val = v1 + v2 + carry
carry = val // 10
val = val % 10
cur.next = ListNode(val) # create new node
# update ptrs
cur = cur.next
l1 = l1.next if l1 else None
l2 = l2.next if l2 else None
return dummy.next

# 或者用快慢指针
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
cur = head
visited = {}
while cur:
if cur in visited: return True
visited[cur] = True
cur = cur.next
return False
Find The Duplicate Number 查找重复编号

class Solution:
def findDuplicate(self, nums: List[int]) -> int:
# 数组的值是[1,n] 0不在数组里面,可以把数组的值当做指针
# 本质上就是一个环,如果存在重复元素
# 如何找到最开始重复的元素:通过弗洛伊德算法 p(慢指针走到环开始节点需要的距离) = x(相交位置走到环开始需要的距离)
slow, fast = 0, 0
# 找到相交位置
while True:
slow = nums[slow]
fast = nums[nums[fast]]
if slow == fast:
break
# 弗洛伊德算法
slow2 = 0
while True:
slow = nums[slow] # 相交位置往前走
slow2 = nums[slow2] # 起始位置往前走
if slow == slow2:
return slow

class Node:
def __init__(self, key, val):
self.key, self.val = key, val
self.next = self.prev = None # 是双向链表
class LRUCache:
def __init__(self, capacity: int):
self.cap = capacity
self.cache = {} # 快速找到节点的hashmap, 同时可以判断队列的长度
# left:LRU right:MRU
self.left, self.right = Node(0, 0), Node(0, 0) # 指向左边第一个节点, 指向右边第一个节点,方便快速插入和删除,并且是双向链表
self.left.next = self.right # 注意这里要更新前后指针
self.right.prev = self.left
# 从队列中删除一个元素
def remove(self, node):
prev, nxt = node.prev, node.next # 这里先把前后节点弄出来
prev.next = nxt
nxt.prev = prev
# 插入队列尾部
def insert(self, node):
prev, nxt = self.right.prev, self.right
prev.next = nxt.prev = node
node.prev, node.next = prev, nxt
def get(self, key: int) -> int:
if key in self.cache:
# 将该元素从原先位置删除
self.remove(self.cache[key])
# 将该元素插入到最后
self.insert(self.cache[key])
return self.cache[key].val # 注意这里是返回值
return -1
def put(self, key: int, value: int) -> None:
if key in self.cache: # 注意这里是判断key是否存在,而不是self.cache[key]值是否存在
# 将该元素删除
self.remove(self.cache[key])
# 更新值,注意这里直接创建了新节点
self.cache[key] = Node(key, value)
# 将新的值插入到最后
self.insert(self.cache[key])
# 判断队列是否已满
if len(self.cache) > self.cap:
# 将左边最后一个元素删除
lru = self.left.next
self.remove(lru)
# 从缓存删除
del self.cache[lru.key]
Tree 🔗︎

错误的示范:
1、需要一个temp保存你要动的指针的值 否则,你把指针直接指到另一个地方了,原先的值你找不到了
2、可以先调换左右子树的,不是非得到叶子结点才能调换
3、递归调用一定是针对左右子树的,不能只递归左子树或者右子树
def test(root):
if not root:
return root
temp = root.left
root.left = root.right
root.right = temp
this.test(root.left)
this.test(root.right)
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
temp = root.left
root.left = root.right
root.right = temp
self.invertTree(root.left)
self.invertTree(root.right)
return root
Maximum Depth of Binary Tree 二叉树的最大深度

这个是最佳的理解树的遍历的范例
# DFS
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
# 层序遍历,没有递归调用
"""
双端队列用来存放每一层的数据, 一开始push到队列里的是根节点,根节点弹出来的时候再推入左右子节点。
上面做完刚好是level1 ,也就是**要先处理上一层节点再处理下一层节点**
q = deque([root])
while q:
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
层序遍历也是BFS, 广度优先搜索
"""
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
q = deque([root]) # 双端队列
level = 0
# 队列非空
while q:
# 要先处理上一层节点再处理下一层节点
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
level += 1
return level
# 迭代法,先序遍历
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
stack = [[root, 1]] #
res = 1
while stack: # 最外层肯定是判断队列是否为空
node, depth = stack.pop()
if node:
res = max(res, depth)
stack.append([node.left, depth + 1]) # 深度是上一个节点+1
stack.append([node.right, depth + 1])
return res

# 本质是和高度相关, 将高度和直径关联上, 从下到上开始遍历
# 暴力解法是从上到下时间复杂度是O(n) * n
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
if not root:
return -1
res = [0]
# 计算子树的高度
def dfs(root):
# nonlocal res 如果是用值的话 需要声明为nonlocal
if not root:
return -1 # 因为单个节点是0
left = dfs(root.left)
right = dfs(root.right)
res[0] = max(res[0], left + right + 2) # left + right + 2是当前节点的直径或者说是最大边
return 1 + max(left, right)
dfs(root)
return res[0]

class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
def dfs(root):
if not root:
return [True, -1]
left = dfs(root.left)
right = dfs(root.right)
balanced = left[0] and right[0] and abs(left[1] - right[1]) <= 1 # 注意这里同时要判断左右子树平衡,这样顶部的节点的平衡才代表了整棵树是否平衡
return [balanced, 1 + max(left[1], right[1])]
return dfs(root)[0]

class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
# 比较单个节点的值是否相等,然后再比较叶子树(叶子树判断是否相等又变成相同的子问题了,可以递归调用判断)
# 比较单个节点
if not p and not q:
return True
if not p or not q or p.val != q.val:
return False
# 节点值相等,再判断叶子树(作为整体判断)
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
from collections import deque
def isSameTree(tr1: TreeNode, tr2: TreeNode) -> bool:
if not tr1 and not tr2:
return True
if not tr1 or not tr2:
return False
s = deque([(tr1, tr2)])
while s:
n1, n2 = s.popleft()
# 当前节点值是否相同
if n1.val != n2.val:
return False
# 检查左子树: 这里的思路可以简单点,如果一个为空,一个非空,肯定返回false。如果都为空,也不需要append
if n1.left and not n2.left or not n1.left and n2.left:
return False
elif n1.left and n2.left:
s.append((n1.left, n2.left))
# 检查右子树
if n1.right and not n2.right or not n1.right and n2.right:
return False
elif n1.right and n2.right:
s.append((n1.right, n2.right))
return True
Subtree of Another Tree 另一棵树的子树

class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not subRoot: return True
if not root: return False
def isSameTree(p, q):
if not p and not q:
return True
if not p or not q or p.val != q.val:
return False
# 节点值相等,再判断叶子树(作为整体判断)
return isSameTree(p.left, q.left) and isSameTree(p.right, q.right)
# 判断当前节点
if isSameTree(root, subRoot):
return True
# 递归判断左右子树是否是子树
# 注意这里不是判断左右子树是否是sameTree,因为左右子树这个时候是同类子问题(递归地考虑问题)
return (self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot))
Lowest Common Ancestor of a Binary Search Tree 二叉搜索树的最低共同祖先

# 注意:这里说了是二叉搜索树, 所以不用考虑每个节点的路径问题
# 直接一个指针往下判断就了事。 不一定都要遍历树
# 从问题出发,而不是从固有的思维出发
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
cur = root
while cur:
# [7,9]
if p.val > cur.val and q.val > cur.val:
cur = cur.right
# [0, 4]
elif p.val < cur.val and q.val < cur.val:
cur = cur.left
# [6, 7]
else:
return cur
Binary Tree Level Order Traversal 二叉树级别顺序遍历

class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
if not root.left and not root.right:
return [[root.val]]
dq = deque([root])
res = []
while dq:
levelArr = []
for i in range(len(dq)):
node = dq.popleft()
levelArr.append(node.val)
if node.left:
dq.append(node.left)
if node.right:
dq.append(node.right)
res.append(levelArr)
return res
Binary Tree Right Side View 二叉树右侧视图

class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return None
dq = deque([root]) # ??
res = []
while dq:
# level
rightSide = None
for i in range(len(dq)):
node = dq.popleft() ## ?
rightSide = node # 用一个变量保存最后一个值,不用判断是否是最后一个元素因为for循环自动会执行到最后
if node.left:
dq.append(node.left)
if node.right:
dq.append(node.right)
res.append(rightSide.val)
return res
Count Good Nodes In Binary Tree 计算二叉树中的良好节点

class Solution:
def goodNodes(self, root: TreeNode) -> int:
# 一看就是要深度遍历,但是有一个点是先序遍历获得当前最大值的节点。如果后续的节点比它小,肯定不是good节点
def dfs(root, maxVal):
if not root:
return 0 # 空节点
res = 1 if root.val >= maxVal else 0 # 计算good nodes的个数
maxv = max(root.val, maxVal)
res += dfs(root.left, maxv) # 递归计算子树的good nodes的节点数
res += dfs(root.right, maxv)
return res
return dfs(root, root.val) # 根节点始终是good nodes
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
# 注意:仔细看边界case, 你会发现,不能单纯对比左右子树和父节点的关系。
# BST的定义是 右子树的所有节点都必须大于节点
# 所有右子树需要把节点当做 左区间
def dfs(root, left, right):
if not root:
return True
if not (root.val < right and root.val > left):
return False
return dfs(root.left, left, root.val) and dfs(root.right, root.val, right) #这里left是当前节点的左区间
return dfs(root, float('-inf'), float('inf'))
Kth Smallest Element In a Bst Bst 中第 k 个最小元素

class Solution:
def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
# 这里是BST,所以一定会想到中序遍历输出是刚好排序好的
# 因为有堆栈,这里可以用迭代法
stack = []
cur = root
num = 0
while cur or stack: # 这里是or判断只要有一个存在
while cur:
stack.append(cur)
cur = cur.left
# 处理节点
cur = stack.pop() # 这里pop出来是按照从小到大的
num += 1
if num == k:
return cur.val
cur = cur.right
Construct Binary Tree From Preorder And Inorder Traversal 从预序和无序遍历构造二叉树

class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
# 先序遍历的节点一定是根节点。 然后通过中序遍历的划分左右子树
# 注意这里要判断空的情况
if not preorder or not inorder:
return None
# 创建根节点
root = TreeNode(preorder[0])
mid = inorder.index(preorder[0])
# 递归的思路创建左右子树
root.left = self.buildTree(preorder[1:mid + 1], inorder[:mid]) # 注意这里mid+1不包含。 这里是将中序和先序的节点做了划分
root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
return root
给定一个整数 N,找出可以用 1 到 N 的值制作的唯一二叉搜索树(BST)的总数。
输入:
n = 3
输出:5
解释: 对于n = 3,可能的前序遍历结果为:1 2 31 3 22 1 33 1 23 2 1
输入:
n = 4
输出:14
BST(Binary Search Tree,二叉搜索树)是一种特殊的二叉树,满足以下条件:
- 每个节点的值都小于其右子树中所有节点的值。
- 每个节点的值都大于其左子树中所有节点的值。
例如,对于节点集合 {1, 2, 3},可以构造出以下几种不同的 BST:


为了计算具有 n 个节点的唯一 BST 的数量,我们可以通过递归和动态规划的方法来解决问题。
基本情况:
- 当
n = 1时,只有一个节点,显然只有一种情况:T(1) = 1。 - 当
n = 2时,有两个节点,有两种情况:T(2) = 2。
- 当
一般情况:
- 假设当前有
n个节点,选择某个节点i作为根节点。- 左子树包含比
i小的所有节点(即1到i-1),共有T(i-1)种组合。 - 右子树包含比
i大的所有节点(即i+1到n),共有T(n-i)种组合。 - 因此,以
i为根节点的 BST 总数为:T(i-1) * T(n-i)。
- 左子树包含比
- 遍历所有可能的根节点
i(从1到n),将结果累加即可得到总数量: [ T(n) = \sum_{i=1}^{n} T(i-1) \times T(n-i) ]
- 假设当前有
当
n = 3时:- 假设
1是根节点:T(0) * T(2) = 1 * 2 = 2。 - 假设
2是根节点:T(1) * T(1) = 1 * 1 = 1。 - 假设
3是根节点:T(2) * T(0) = 2 * 1 = 2。 - 总数为:
2 + 1 + 2 = 5。
- 假设
当
n = 4时:- 假设
1是根节点:T(0) * T(3) = 1 * 5 = 5。 - 假设
2是根节点:T(1) * T(2) = 1 * 2 = 2。 - 假设
3是根节点:T(2) * T(1) = 2 * 1 = 2。 - 假设
4是根节点:T(3) * T(0) = 5 * 1 = 5。 - 总数为:
5 + 2 + 2 + 5 = 14。
- 假设
方法 1:暴力递归 通过递归的方式计算每个节点作为根节点的情况。以下是 JavaScript 实现:
// i is the root, n is the total nodes' number
const G = (i, n) => {
return fn(i - 1) * fn(n - i);
};
// Get the total number of BST trees with n nodes.
const fn = (n) => {
let _ = 0;
if (n === 0 || n === 1) return 1;
for (let i = 1; i <= n; i++) {
_ += G(i, n);
}
return _;
};
console.log(fn(3)); // 输出: 5
递归树如下所示:
f(3)
├── G(1,3) -> f(0) * f(2)
├── G(2,3) -> f(1) * f(1)
└── G(3,3) -> f(2) * f(0)
可以看到,f(1) 和 f(2) 被重复计算,导致效率低下。
方法 2:带缓存的递归 为了避免重复计算,我们可以使用缓存存储中间结果。
// get the total number of BST tress with i as the root node
const G = (i, n) => {
return fn(i - 1) * fn(n - i);
};
const dp = [];
const fn = (n) => {
let _ = 0;
if (n === 0 || n === 1) return 1;
if (dp[n]) {
console.log("hit cache");
return dp[n];
}
// loop all nodes
for (let i = 1; i <= n; i++) {
// add them all
_ += G(i, n);
}
// cache result
dp[n] = _;
return _;
};
console.log(fn(3)); // 输出: 5
方法 3:动态规划(最优解) 通过自底向上的方式构建 DP 表,避免递归开销。
const getNumberOfBSTs = (n) => {
const T = [];
T[0] = 1; // Base case: 0 nodes -> 1 BST (empty tree)
T[1] = 1; // Base case: 1 node -> 1 BST
for (let i = 2; i <= n; i++) {
T[i] = 0; // Initialize current value
for (let j = 1; j <= i; j++) {
// Calculate the number of BSTs with j as the root
T[i] += T[j - 1] * T[i - j];
}
}
return T[n]; // Return the result for n nodes
};
console.log(getNumberOfBSTs(3)); // 输出: 5
console.log(getNumberOfBSTs(4)); // 输出: 14
暴力递归:
- 时间复杂度:O(2^n),因为每次递归都会分裂成两个子问题。
- 空间复杂度:O(n),递归栈的深度。
带缓存的递归:
- 时间复杂度:O(n^2),因为每个状态只会被计算一次。
- 空间复杂度:O(n),用于存储缓存。
动态规划:
- 时间复杂度:O(n^2),双层循环。
- 空间复杂度:O(n),用于存储 DP 表。
Trie 🔗︎
Implement Trie Prefix Tree 实现 Trie 前缀树

# 前缀树判断字符串前缀的特别高效,因为这个每一层的字符是固定的 比如26个字符 时间复杂度就是字符集的大小
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word: str) -> None:
cur = self.root
for c in word: # 遍历字符串
if c not in cur.children:
cur.children[c] = TrieNode()
cur = cur.children[c] # 移动到下一个指针
cur.isEndChar = True
def search(self, word: str) -> bool:
cur = self.root
for c in word:
if c not in cur.children:
return False
cur = cur.children[c]
return cur.isEndChar # 最后一个字符串
def startsWith(self, prefix: str) -> bool:
cur = self.root
for c in prefix:
if c not in cur.children:
return False
cur = cur.children[c]
return True
Design Add And Search Words Data Structure 设计添加和搜索单词数据结构

# 卡点是:如何递归地思考解决问题的方式 递归本质就是判定是否是相同子问题,如果是,则调用它即可
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word: str) -> None:
cur = self.root
for c in word: # 遍历字符串
if c not in cur.children:
cur.children[c] = TrieNode()
cur = cur.children[c] # 移动到下一个指针
cur.isEndChar = True
def search(self, word: str) -> bool:
def isFind(offset, node):
cur = node
for i in range(offset, len(word)):
c = word[i]
if c != '.':
if c not in cur.children:
return False
cur = cur.children[c]
else:
# 需要判断所有子节点
for child in cur.children.values():
if isFind(i + 1, child):
return True
# 如果没找到匹配的
return False
return cur.isEndChar
return isFind(0, self.root) # 最后一个字符串
class WordDictionary:
def __init__(self):
self.trie = Trie()
def addWord(self, word: str) -> None:
self.trie.insert(word)
def search(self, word: str) -> bool:
return self.trie.search(word)
backtracking 🔗︎
# openN < 3, closeN < 3
# openN > closeN can add ')'
# openN == closeN == 3, exit
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
stack = []
res = []
# 整个递归调用,就是我们画出来的决策树。递归调用的参数就是我们核心考虑的两个变量,左括符和右括符的数量
def backtrack(openN, closeN): # 回溯
if openN == closeN == n:
res.append("".join(stack)) # 理解 Python 的 join 是先选定一个“模板”或“胶水”,再告诉列表“请用它来拼装自己”
return
# 发现没有,回溯会调用两次递归调用。 每次都是一个新的尝试。而且要恢复现场
# 这里的恢复现场时对堆栈的恢复
if openN < n:
stack.append('(')
backtrack(openN+1, closeN)
stack.pop() # 回溯恢复现场,保证递归的其他分支状态正确
if openN > closeN: # 保证有效组合的关键逻辑,这里其实对树进行了 ** 剪枝 ** ,对无效组合避免了递归调用
stack.append(')')
backtrack(openN, closeN+1)
stack.pop()
backtrack(0, 0)
return res
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
# 这里的卡点是: 对回溯法不是很理解
# 回溯其实就是递归树或者叫决策树,每个节点做决策。 如果用暴力求解时间复杂度会很高
# 2^n个排列组合,然后我们的数组长度是n, 我们需要遍历数组尝试每种情况,时间复杂度是n * 2^n
res = []
subsets = []
def dfs(i): # 这里的i表示数组的索引
if i >= len(nums): # 表示每个元素都决策完成
res.append(subsets.copy()) # 注意这里必须要用复制,因为subsets每次执行dfs时候都会被修改
return
# 决策加入 nums[i]
subsets.append(nums[i])
# 然后递归决策下一个元素
dfs(i + 1)
# 或者决策不加入 恢复现场也是对堆栈的恢复
subsets.pop()
dfs(i + 1)
dfs(0)
return res

class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
# 还是决策树
res = []
def dfs(cur, i, total): # 这里我们需要当前节点的和是多少, nums的指针i, 当前结果cur
# 处理基本case
if total == target:
res.append(cur.copy()) # 注意这里要复制cur,因为每次都会修改这个变量
return # 结束递归
if i >= len(candidates) or total > target:
return # 结束递归
# 包含当前节点
cur.append(candidates[i])
# 递归决策
dfs(cur, i, total + candidates[i]) ## 注意这里i保留不变,因为还可以用 total要变化
# 不包含当前节点
cur.pop()
dfs(cur, i + 1, total) # 这里的i要+1 ,因为不包含 total不变化
dfs([], 0, 0)
return res
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
# 从顶到底画出递归树, 然后从底部上来,重新建立排列组合
result = []
# 处理只有一个元素。
if len(nums) == 0:
return [nums.copy()]
for i in range(len(nums)):
num = nums.pop(0) # 把第一个元素删掉
perms = self.permute(nums) # 然后递归球剩下的元素的排列组合
for i in perms:
perm = i.append(num) # 这里的i是数组 针对每个组合,把删掉的元素拼接回来
result.extend(perms) # 获得组合
nums.append(num) # 将原先删掉的元素拼接回来
return result

class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
# 关键是跳过重复的元素,避免重复组合
res = []
nums.sort() # 保证重复的元素在一起
def backtracking(i, subset): # subset是每次递归的结果
if i == len(nums): # 指针到最后
return res.append(subset[::]) # 复制集合
# include current
subset.append(nums[i])
backtracking(i + 1, subset) # 递归左子树
subset.pop() # 恢复subset的值
# not include current
while i + 1 < len(nums) and nums[i] == nums[i + 1]: # 跳过重复元素
i += 1
backtracking(i + 1, subset) # 递归右子树
backtracking(0, [])
return res

class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
# 关键点是:这里的区别是存在重复元素,所以不能简单用决策树
# 需要
candidates.sort()
res = []
def backtracking(cur, pos, target): # cur是当前结果
# 基本情况
if target == 0:
res.append(cur.copy())
if target <= 0:
return
prev = -1
for i in range(pos, len(candidates)): # 这里是关键点,需要跳过重复的节点,继续调用backtracking, 如果没有重复的就不需要这个for循环了
if prev == candidates[i]:
continue
# 包含该元素
cur.append(candidates[i])
backtracking(cur, i + 1, target - candidates[i]) # 遍历左右子树
cur.pop() # 递归返回
prev = candidates[i]
backtracking([], 0, target)
return res
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
rows, cols = len(board), len(board[0])
path = set()
def dfs(r, c, i):
if i == len(word):
return True
if (r < 0 or c < 0 or
r >= rows or c >= cols or
word[i] != board[r][c] or
(r, c) in path):
return False
path.add((r,c))
res = (dfs(r + 1, c, i + 1) or
dfs(r - 1, c, i + 1) or
dfs(r, c+1, i + 1) or
dfs(r, c-1, i + 1))
path.remove((r,c))
return res
for r in range(rows):
for c in range(cols):
if dfs(r,c,0): return True

class Solution:
def partition(self, s: str) -> List[List[str]]:
res = []
part = []
def dfs(i):
if i >= len(s):
res.append(part.copy())
return
for j in range(i, len(s)):
if self.isPal(s, i, j):
part.append(s[i:j + 1])
dfs(j + 1)
part.pop()
dfs(0)
return res
def isPal(self, s, l, r):
while l < r:
if s[l] != s[r]:
return False
l, r = l + 1, r - 1
return True
Letter Combinations of a Phone Number 电话号码的字母组合

class Solution:
def letterCombinations(self, digits: str) -> List[str]:
res = []
digital2Char = {
'2': 'abc',
'3': 'def',
'4': 'ghi',
'5': 'jkl',
'6': 'mno',
'7': 'pqrs',
'8': 'tuv',
'9': 'wxyz'
}
def dfs(i, curStr):
if len(curStr) == len(digits):
res.append(curStr)
return
for c in digital2Char[digits[i]]:
dfs(i + 1, curStr + c)
if digits:
dfs(0, '')
return res
Heap & Priority Queue 🔗︎
class Solution:
def lastStoneWeight(self, stones: List[int]) -> int:
stores = [-s for s in stones]
heapq.heapify(stores)
while len(stores) > 1: # 当堆的元素大于2
first = heapq.heappop(stores)
second = heapq.heappop(stores)
if first < second:
heapq.heappush(stores, first - second) # 注意都是负数
stores.append(0) # 当stores为空的边界case
return abs(stores[0])
Kth Largest Element In a Stream

class KthLargest:
def __init__(self, k: int, nums: List[int]):
self.minHeap, self.k = nums, k
heapq.heapify(self.minHeap) # 时间复杂度是nlogn
while len(self.minHeap) > k:
heapq.heappop(self.minHeap)
def add(self, val: int) -> int:
heapq.heappush(self.minHeap, val)
# 当整个的元素个数比k大的时候,需要从小顶堆删除元素
# logn时间复杂度,如果数组 复杂度是n
if len(self.minHeap) > self.k:
heapq.heappop(self.minHeap)
return self.minHeap[0]
# 时间复杂度时nlogn
class Solution:
def lastStoneWeight(self, stones: List[int]) -> int:
stores = [-s for s in stones]
heapq.heapify(stores)
while len(stores) > 1: # 当堆的元素大于2
first = heapq.heappop(stores)
second = heapq.heappop(stores)
if first < second:
heapq.heappush(stores, first - second) # 注意都是负数
stores.append(0) # 当stores为空的边界case
return abs(stores[0])
Kth Largest Element In An Array

class Solution:
def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
# 关键点用最小堆
# 计算距离
minHeap = []
for x, y in points:
minHeap.append([x**2 + y**2, x, y])
res = []
heapq.heapify(minHeap) # 注意这里的minHeap是[10, 1, 2], [8, 1, 2]
while k > 0:
dist, x, y = heapq.heappop(minHeap)
res.append([x, y])
k -= 1
return res

class Solution:
def leastInterval(self, tasks: List[str], n: int) -> int:
counter = Counter(tasks)
maxHeap = [-cnt for cnt in counter.values()]
heapq.heapify(maxHeap) # 当前要处理的
time = 0
q = deque() # [-cnt, idletime] 暂存还不处理
while maxHeap or q:
time += 1
if maxHeap:
cnt = heapq.heappop(maxHeap) + 1
if cnt: # 如果还有
q.append([cnt, time + n])
if q and q[0][1] == time: # 当到了idle时间,重新放到堆处理
heapq.heappush(maxHeap, q.popleft()[0])
return time
# 堆和hashMap的使用。有些使用技巧,比如堆存了index和count作为时间轴
class Twitter:
def __init__(self):
self.followMap = defaultdict(set) # 自动初始化 userId -> [followeeId]
self.twitterMap = defaultdict(list) # 自动初始化 userId -> [count, twittwerId]
self.count = 0 # 记录发推的id,作为时间的考量
def postTweet(self, userId: int, tweetId: int) -> None:
self.twitterMap[userId].append([self.count, tweetId])
self.count -= 1
def getNewsFeed(self, userId: int) -> List[int]:
minHeap = []
res = []
self.followMap[userId].add(userId)
# 构建堆
for followee in self.followMap[userId]:
if followee in self.twitterMap:
index = len(self.twitterMap[followee]) - 1
count, twitterId = self.twitterMap[followee][index]
heapq.heappush(minHeap, [count, twitterId, followee, index - 1]) # 这里index - 1是为了拿到上一个twittwer
heapq.heapify(minHeap)
while minHeap and len(res) < 10:
count, twitterId, followee, index = heapq.heappop(minHeap)
res.append(twitterId)
if index >= 0:
# 取上一条
count, twitterId = self.twitterMap[followee][index]
heapq.heappush(minHeap, [count,twitterId,followee,index-1])
return res
def follow(self, followerId: int, followeeId: int) -> None:
self.followMap[followerId].add(followeeId)
def unfollow(self, followerId: int, followeeId: int) -> None:
if followeeId in self.followMap[followerId]:
self.followMap[followerId].remove(followeeId)
给定一个数组和一个整数 k,其中 k 小于数组的长度,我们需要找到数组中第 k 小的元素。假设数组中的所有元素都是不同的。
输入:
arr[] = {7, 10, 4, 3, 20, 15}
k = 3
输出:
7
输入:
arr[] = {7, 10, 4, 3, 20, 15}
k = 4
输出:
10
通过将数组排序后,直接返回第 k 小的元素。
实现代码 🔗︎
function getKthSmallest(arr: number[], k: number): number {
const sortedArr = arr.sort((a, b) => a - b); // 升序排序
return sortedArr[k - 1]; // 返回第 k 小的元素
}
- 排序的时间复杂度为 O(n log n),其中
n是数组的长度。 - 空间复杂度为 O(1)(如果原地排序)或 O(n)(如果创建了新数组)。
可以使用堆来优化查找第 k 小元素的过程,避免对整个数组进行排序。
- 小顶堆:
- 构建一个小顶堆,依次弹出堆顶元素
k-1次,最后堆顶即为第k小的元素。 - 时间复杂度为 O(n + k log n)。
- 构建一个小顶堆,依次弹出堆顶元素
- 大顶堆:
- 构建一个大小为
k的大顶堆,遍历数组时维护堆的大小。 - 如果当前元素小于堆顶元素,则替换堆顶并调整堆。
- 最终堆顶即为第
k小的元素。 - 时间复杂度为 O(n log k)。
- 构建一个大小为
function getKthSmallestUsingHeap(arr: number[], k: number): number {
const maxHeap = new MaxHeap();
for (let i = 0; i < arr.length; i++) {
if (maxHeap.size() < k) {
maxHeap.insert(arr[i]); // 插入堆中
} else if (arr[i] < maxHeap.peek()) {
maxHeap.extractMax(); // 移除堆顶
maxHeap.insert(arr[i]); // 插入新元素
}
}
return maxHeap.peek(); // 堆顶即为第 k 小元素
}
// 假设 MaxHeap 是一个实现好的大顶堆类
class MaxHeap {
private heap: number[] = [];
insert(value: number) {
this.heap.push(value);
this.heapifyUp(this.heap.length - 1);
}
extractMax(): number {
const max = this.heap[0];
this.heap[0] = this.heap[this.heap.length - 1];
this.heap.pop();
this.heapifyDown(0);
return max;
}
peek(): number {
return this.heap[0];
}
size(): number {
return this.heap.length;
}
private heapifyUp(index: number) {
while (index > 0) {
const parentIndex = Math.floor((index - 1) / 2);
if (this.heap[parentIndex] >= this.heap[index]) break;
[this.heap[parentIndex], this.heap[index]] = [this.heap[index], this.heap[parentIndex]];
index = parentIndex;
}
}
private heapifyDown(index: number) {
while (true) {
const leftChildIndex = 2 * index + 1;
const rightChildIndex = 2 * index + 2;
let largestIndex = index;
if (leftChildIndex < this.heap.length && this.heap[leftChildIndex] > this.heap[largestIndex]) {
largestIndex = leftChildIndex;
}
if (rightChildIndex < this.heap.length && this.heap[rightChildIndex] > this.heap[largestIndex]) {
largestIndex = rightChildIndex;
}
if (largestIndex === index) break;
[this.heap[index], this.heap[largestIndex]] = [this.heap[largestIndex], this.heap[index]];
index = largestIndex;
}
}
}
- 构建堆:
O(n log k)。 - 空间复杂度:
O(k)(堆的大小限制为k)。
interval 🔗︎

class Solution:
def insert(self, intervals: List[List[int]], newInterval: List[int]) -> List[List[int]]:
# 本质上要判断是否重叠, 先想清楚所有情况,归纳以下,不要一个个枚举,代码乱的一批
res = []
for i in range(len(intervals)):
if newInterval[1] < intervals[i][0]: # 在左边
res.append(newInterval)
return res + intervals[i:] # 合并所有后面的结果
elif newInterval[0] > intervals[i][1]: # 在右边
res.append(intervals[i])
else: # 重叠了,进行合并
newInterval = [min(newInterval[0], intervals[i][0]), max(newInterval[1], intervals[i][1])]
# 如果没有命中上面的在左边的条件,确保newInterval会插入
res.append(newInterval)
return res

# 没有黑科技,就是正常思维
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort(key = lambda i:i[0])
output = [intervals[0]]
for start, end in intervals[1:]:
lastEnd = output[-1][1]
if start <= lastEnd: # 有重叠需要合并
output[-1][1] = max(output[-1][1], end)
else:
output.append([start, end])
return output
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
# 关键点是要对输入排序
# 然后如果相邻的两个重叠了。 需要保留end更小的那个,因为这样重叠的可能性更小
intervals.sort()
res = 0
prevEnd = intervals[0][1] # 要保留前面合并的end
for start, end in intervals[1:]:
if start >= prevEnd: # 没有重叠
prevEnd = end
else:
res += 1
prevEnd = min(end, prevEnd) # 移除一个。这里没有真正移出,只是合并了
return res
Greedy 🔗︎

# 这里用了贪心算法啊,就是当你对总的和没有帮助 都归0了或者负数了,就舍弃了。因为你对判断最大的和没有帮助
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
maxSum = nums[0] # 记录当前的最大和
curSum = 0 # 计算和
for i in nums:
if curSum < 0: # 如果对和没有帮助,直接去掉
curSum = 0
curSum += i
maxSum = max(curSum, maxSum)
return maxSum

class Solution:
def canJump(self, nums: List[int]) -> bool:
# 是一个dp问题,可以通过穷举法
# 这个最差的时间复杂度是n^n次方,因为这是一个决策树,用它或者不用它是2^n。 这里的分支是n,所以是n^n
# 通过缓存重复计算可以将时间复杂度到n^2 ( 为什么是n^2, 因为缓存基于你上次访问的,是两次for遍历)
# 贪心算法时间复杂度可以达到n
# 贪心算法核心是从右到左,判断最后一个元素能否到下一个目标
goal = len(nums) - 1
for i in range(len(nums)-1, -1, -1): # 从后到左,步长是-1
if i + nums[i] >= goal: #说明上一个数可以到终点,我们把终点往前移动一位
goal = i
return True if goal == 0 else False

class Solution:
def jump(self, nums: List[int]) -> int:
# 关键点是计算当前能跳的最远距离的是多少。然后计算每个区块的个数,就是跳的次数
res = 0
l = 0 # 移动窗口
r = 0
fartest = 0
while r < len(nums) - 1: # 没有到达终点
# BFS遍历,能跳的最远的距离是多少
for i in range(l, r + 1):
fartest = max(i+nums[i], fartest)
l = r + 1 # 更新滑动窗口
r = fartest
# 每次更新滑动窗口,表示跳跃的次数
res += 1
return res
# 直觉的解法 。有点难理解
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
if sum(gas) < sum(cost):
return -1
total = 0
res = 0
for i in range(len(gas)):
total += (gas[i] - cost[i])
if total < 0:
total = 0 # 重置
res = i + 1 # 下一个
return res
class Solution:
def isNStraightHand(self, hand: List[int], groupSize: int) -> bool:
# 关键点是:每次都取最小的值,然后组一组,如果组成功了。 把这个值的个数减掉。
# 要统计每个值的数量
if len(hand) % groupSize:
return False
count = {} # 或者用Counter
for i in hand:
count[i] = 1 + count.get(i, 0)
# 把key都组装成堆
minHeap = list(count.keys())
heapq.heapify(minHeap)
while minHeap:
first = minHeap[0]
for i in range(first, first + groupSize):
if i not in count: # 如果在hashmap中没找到 说明没有组成成功
return False
count[i] -= 1 # 组成成功数量减去一
if count[i] == 0: # 这个数字已经组完成了
if i != minHeap[0]: # 说明组成的这个数已经不是最小的数了,出现了漏数的情况
return False
heapq.heappop(minHeap)
return True
Merge Triplets to Form Target Triplet
class Solution:
def mergeTriplets(self, triplets: List[List[int]], target: List[int]) -> bool:
res = set() # 去掉重复的
for i in triplets:
if i[0] > target[0] or i[1] > target[1] or i[2] > target[2]: # 剔除掉大于target的元素
continue
# 满足条件
for index, v in enumerate(i):
if v == target[index]: # 说明包含了target的元素
res.add(index)
# 因为剔除了大于的,剩下的一定是小于等于的。如果等于的能找到三个 说明一定能找到
return len(res) >= 3

class Solution:
def partitionLabels(self, s: str) -> List[int]:
# 不是用滑动窗口,不要思维定势了。这里用hashmap保存每个字母的最后索引
# 判断前面字符的索引是否小于这个最后索引,如果小于,说明还不能分区
# end: 记录当前分区的最后索引。
hashmap = {} # char -> last index of s
for i, v in enumerate(s):
hashmap[v] = i
res = []
size = 0 # 记录分区的长度
end = 0 # 记录当前结束的位置
for i, v in enumerate(s):
size += 1
if hashmap[v] > end: # 更新当前分区最长的位置
end = hashmap[v]
if i == end: # 说明已经达到最远的距离了
res.append(size) # 不需要更新end,因为后面都是不同的字符了,会自动更新
size = 0 # 重新开始分区
return res

class Solution:
def checkValidString(self, s: str) -> bool:
# 贪心算法:
# leftMin 当*为空的情况下 (数量最少是
# leftMax 当*为(的情况下 (数量最多的情况是
# 每次遇到)或者* 都会更新这两个值。
# 只有当leftMin为0时,说明刚好匹配
# 当leftMax为负数,说明不匹配
# dp算法 针对*通过决策树判断每种情况
leftMin, leftMax = 0, 0
for i in s:
if i == "*":
leftMin -= 1
leftMax += 1
if i == '(':
leftMin += 1
leftMax += 1
if i == ')':
leftMin -= 1
leftMax -= 1
if leftMin < 0: # 当leftMin小于0 说明不符合要求 重置为0
leftMin = 0
if leftMax < 0:
return False
return leftMin == 0
1-DP 🔗︎


class Solution:
def climbStairs(self, n: int) -> int:
# 关键是决策时每次都是重复决策,我们把上一次决策的信息存储起来。避免重复计算
# 这里就是计算有多少种走法。正常决策树dfs是2^n时间复杂度
# 但是通过dp计算,我们只需要走一遍。从底部计算已经计算过的值。
one, two = 1, 1
for i in range(n-1): # 遍历楼梯数量。画图出来就清楚了
temp = one
one = one + two
two = temp
return one


class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
# 本质上是需要将决策树转为dp数组
# 从最简单的case
# 时间复杂度是O(n) 这里的n其实就是子问题的个数
cost.append(0)
for i in range(len(cost) - 3, -1, -1):
# 计算最小代价
cost[i] = min(cost[i] + cost[i+1], cost[i] + cost[i+2])
return min(cost[0], cost[1])
Graph 🔗︎
给定一个无向图,如何检查图中是否有一个环?
输入:
n = 4(顶点数)e = 4(边数)- 边集合:
{ 0-1, 1-2, 2-3, 0-2 }
输出:
Yes(存在环)示例:
 图:存在环
图:存在环输入:
n = 4(顶点数)e = 3(边数)- 边集合:
{ 0-1, 1-2, 2-3 }
输出:
No(不存在环)示例:
 图:不存在环
图:不存在环
我们都知道:
算法 + 数据结构 = 程序
因此,我们需要创建一个数据结构来表示无向图。以下是两种常见的数据结构:
邻接表
如果顶点1与顶点2和3相连,则邻接表表示为:{ 1: [2, 3] }邻接矩阵
在 JavaScript 中,可以使用Map实现。
方案 1: 并查集(Disjoint Set Union, DSU)
- 初始化: 每个顶点都是一个独立的集合。
- 合并操作: 遍历所有边,如果两个顶点属于不同集合,则合并它们。
- 判断环: 如果两个顶点已经属于同一个集合,则说明存在环。
方案 2: 深度优先搜索(DFS)或广度优先搜索(BFS)
- 访问标记: 使用一个布尔数组记录每个节点是否被访问过。
- 判断环: 如果当前节点的邻接节点已被访问且不是其父节点,则说明存在环。
以下代码实现了基于邻接表的无向图,并提供了三种检测环的方法:并查集、DFS 和 BFS。
/*
Graph using adjacency list. Support operations:
1. Traverse by DFS/BFS
2. hasCircleByDfs
3. hasCircleByBfs
4. hasCircleByDss (Disjoint Set)
*/
class Graph {
constructor() {
this.allVertexes = [];
this.allEdges = [];
this.adList = new Map();
}
// 添加顶点
addV(v) {
if (!this.adList.has(v)) {
this.adList.set(v, []);
}
this.allVertexes.push(v);
}
// 添加边
addE(source, dest) {
if (!this.adList.has(source)) {
this.addV(source);
}
if (!this.adList.has(dest)) {
this.addV(dest);
}
this.adList.get(source).push(dest);
this.adList.get(dest).push(source);
this.allEdges.push({ source, dest });
}
// 删除顶点
removeV(v) {
for (let adV of this.adList.get(v)) {
this.removeE(v, adV);
}
this.adList.delete(v);
}
// 删除边
removeE(source, dest) {
this.adList.set(
source,
this.adList.get(source).filter((v) => v !== dest)
);
this.adList.set(
dest,
this.adList.get(dest).filter((v) => v !== source)
);
}
// 打印邻接表
print() {
for (let v of this.adList.keys()) {
let cons = "";
for (let dest of this.adList.get(v)) {
cons += dest + " ";
}
console.log(v + " -> " + cons);
}
}
// 使用并查集检测环
hasCircleByDss() {
const dss = new DisjointSet();
this.allVertexes.forEach((v) => {
dss.makeSet(v);
});
return this.allEdges.some((e) => dss.union(e.source, e.dest));
}
// 使用 BFS 检测环
bfs(start) {
const queue = [start];
const result = [];
const visited = {};
visited[start] = true;
while (queue.length) {
const curV = queue.shift();
result.push(curV);
this.adList.get(curV).forEach((dest) => {
if (!visited[dest]) {
visited[dest] = true;
queue.push(dest);
}
});
}
return result;
}
hasCircleByBfs() {
const parent = {};
const visited = {};
const queue = [];
for (let i = 0; i < this.allVertexes.length; i++) {
const node = this.allVertexes[i];
if (!visited[node]) {
visited[node] = true;
queue.push(node);
while (queue.length) {
const curV = queue.shift();
visited[curV] = true;
const allAdNodes = this.adList.get(curV);
for (let j = 0; j < allAdNodes.length; j++) {
const dest = allAdNodes[j];
if (!visited[dest]) {
visited[dest] = true;
parent[dest] = curV;
queue.push(dest);
} else if (dest !== parent[curV]) {
return true;
}
}
}
}
}
return false;
}
// 使用 DFS 检测环
dfsRecursive(start) {
const result = [];
const visited = {};
const adList = this.adList;
(function dfs(v) {
if (!v) return null;
visited[v] = true;
result.push(v);
adList.get(v).forEach((dest) => {
if (!visited[dest]) {
return dfs(dest);
}
});
})(start);
return result;
}
dfsIterative(start) {
const result = [];
const visited = {};
const stack = [start];
visited[start] = true;
while (stack.length) {
const curV = stack.pop();
result.push(curV);
this.adList.get(curV).forEach((dest) => {
if (!visited[dest]) {
visited[dest] = true;
stack.push(dest);
}
});
}
return result;
}
hasCircleUtil(node, visited, parent) {
visited[node] = true;
const adList = this.adList.get(node) || [];
for (let i = 0; i < adList.length; i++) {
if (adList[i] === parent) continue;
if (visited[adList[i]]) return true;
const hasCycle = this.hasCircleUtil(adList[i], visited, node);
if (hasCycle) return true;
}
return false;
}
hasCircleByDfs() {
const visited = {};
const allV = this.allVertexes;
for (let i = 0; i < allV.length; i++) {
if (visited[allV[i]]) continue;
const flag = this.hasCircleUtil(allV[i], visited, null);
if (flag) return true;
}
return false;
}
}
// 并查集实现
class DisjointSet {
constructor() {
this.map = new Map();
}
makeSet(data) {
this.map.set(data, -1);
}
find(x) {
const parent = this.map.get(x);
if (parent < 0) {
return x;
} else {
return this.find(this.map.get(x));
}
}
union(x, y) {
const xparent = this.find(x);
const yparent = this.find(y);
if (xparent !== yparent) {
this.map.set(xparent, this.map.get(xparent) + this.map.get(yparent));
this.map.set(yparent, xparent);
} else {
return true;
}
}
console_print() {
console.log(JSON.stringify([...this.map.entries()]));
}
}
// 测试代码
const g = new Graph();
const vertices = ["A", "B", "C", "D", "E", "F"];
for (const v of vertices) {
g.addV(v);
}
g.addE("A", "B");
g.addE("A", "D");
g.addE("B", "C");
g.addE("D", "E");
g.addE("E", "F");
g.addE("A", "E"); // 添加环
g.print();
console.log("Has Circle (DSS):", g.hasCircleByDss());
console.log("Has Circle (DFS):", g.hasCircleByDfs());
console.log("Has Circle (BFS):", g.hasCircleByBfs());
| 方法 | 时间复杂度 |
|---|---|
| BFS/DFS | O(V + E) |
| 并查集 | O(n) → O(log n)(使用路径压缩和按秩合并优化后) |